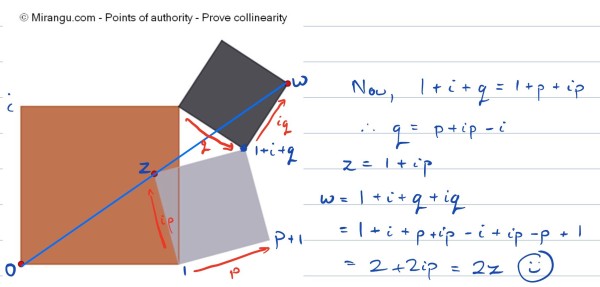
Three squares and three shared vertices. Prove the three red vertices are collinear.
Scroll down for a solution to this problem.
Solution
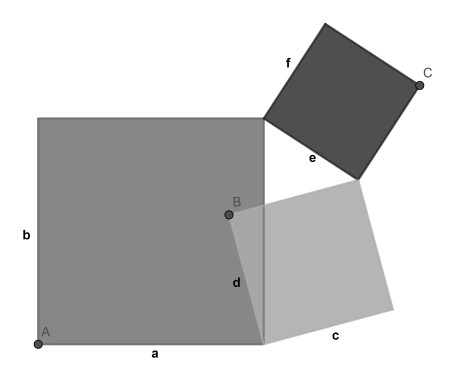
This solution uses vector algebra and rotational symmetry. First assign vectors to the sides of the three squares as shown. They are either pointing up or right. The constraint of the three shared vertices can be written as b=d+c–e.
Now if we rotate over 90° counter clockwise the vectors transform as follows:
| Vector | After 90° rotation |
| a | b |
| b | –a |
| c | d |
| d | –c |
| e | f |
| f | –e |
Now rotating the constraint equation we get: –a=-c+d–f, which can be rewritten as a+d=c+f. Looking at the diagram we see that this means that AB=BC. Since this are vectors, this implies that their direction is the same and hence A, B and C are on a line. As a bonus we get that B is exactly halfway between A and C.