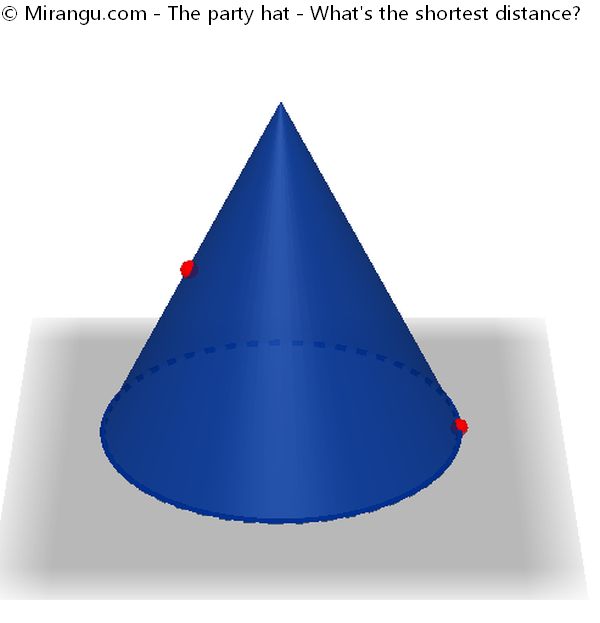
A cone has height 6 and base diameter 6. On it lie two points, one exactly halfway up, the other diametrically opposed at the base. What’s the shortest distance between these points going along the cone surface?
Scroll down for a solution to this problem.
Solution
The shortest path is √(45*(5/4-cos(180/√5))), which is approximately 6,99.
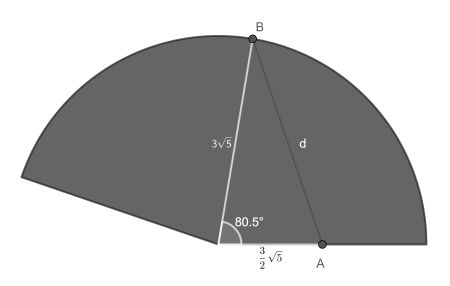
The trick is to fold out the cone to a flat surface and then to draw a straight line from A to B. It will be a circular sector, of which the radius can be found by the Pythagorean Theorem as √(h2+r2), where h is the height and r the radius of the base circle. So in our case 3√5.
The angle of the circular sector can be found by equating the ground circle perimeter to the arc length. So in this case α3√5=360*3, hence α=360/√5, which is approximately 161°.
Now the straight line from A to B, with length d, forms a triangle with the segments to the cone apex, as shown above. These segments have known length and their angle is half that of the total circular sector, since they lie diametrically across.
The final step is applying the cosine rule to determine d. So d2=(3√5)2+(3√5/2)2-2*3√5*3√5/2*cos(π/√5).
Professor Ignacio Larrosa Cañestro has made a three-dimensional animation of the path. It’s a striking fact that the first part leaving A is uphill, while point B is at ground level.