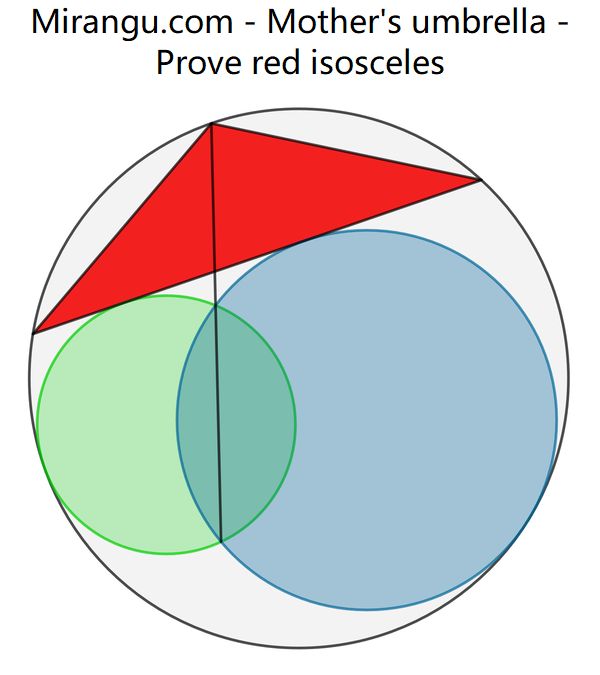
A circle containing two internally tangent circles. Prove that the red triangle is isosceles.
Scroll down for a solution to this problem.
Solution
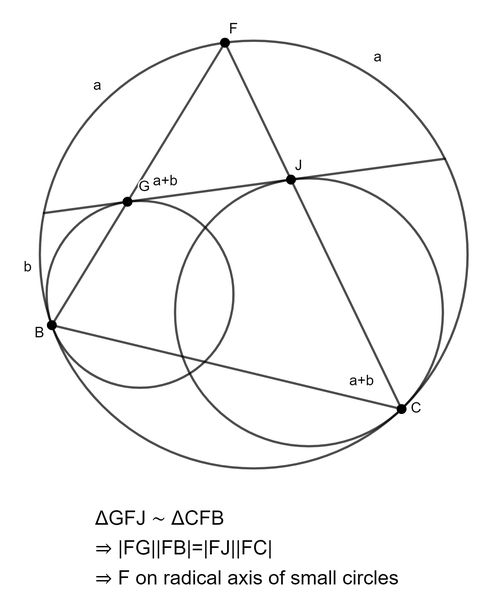
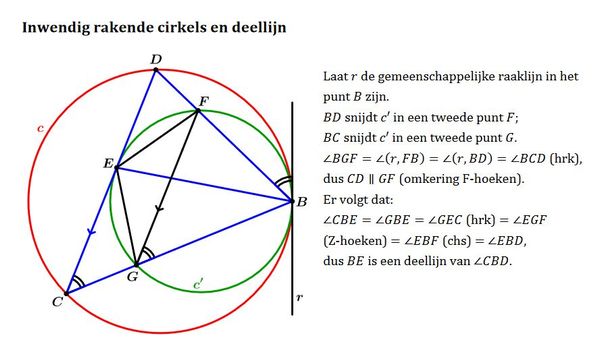
This solution makes use of the lemma below, attributed to Archimedes, showing that F is the midpoint of the arc formed by the tangent chord.
Video
Please find here the video solution: Video: Mother’s umbrella.
2 replies on “Mother’s umbrella”
Dilation of the green circle from the point L to the red circle shows that the horizontal blue tangents are parallel. Then the three angles marked alpha are equal, and the triangles CEM ~LEC are similar. Thus EL*EM = EC^2, and the power of E with respect to any “green-like” circle is the same. This means the radical axis for any pair of intersecting “green-like” circles must go through the point E.
Bravo, very elegant proof!