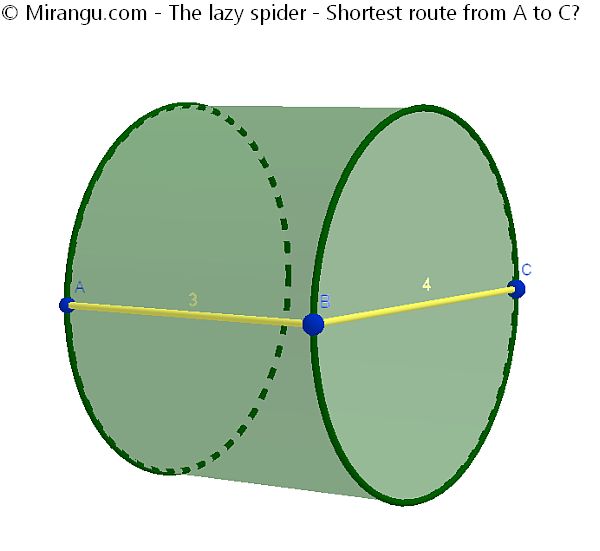
A spider situated at point A on the outside of a cylinder with diameter 4 and height 3 is trying to get to a fly at point C on the complete opposite side as fast as possible. What is the shortest route?
Scroll down for a solution to this problem.
Solution
The shortest route from A to C is √(9+4π2), which is approximately 6,96.
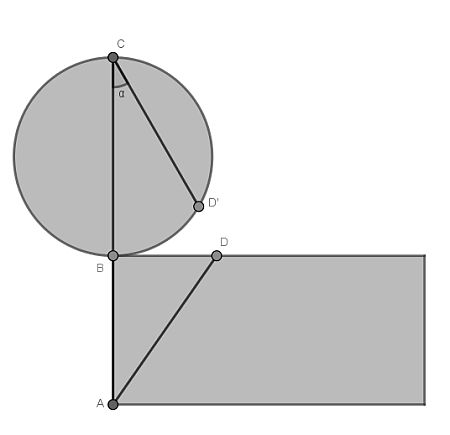
Let’s take a general route from A to a point D on the other edge and further from D to C, where on both the side and the top of the cylinder a straight line is used. It is left as to the reader to find that the total distance is D(α)=√(9+16α2)+4cos(α) where α is in [0,π/2].
It remains a matter of differential calculus to find the minimum of this function on the given interval. It turns out that this is when α=π/2, so when the complete route is on the side of the cylinder.
Note that the side route is only slightly shorter than going via B. If the height would have been a little less, this would have been the shortest one.