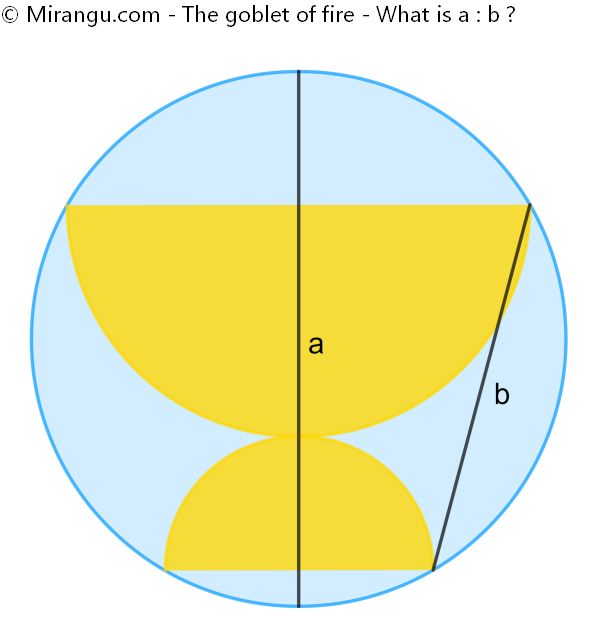
A circle containing two touching semicircles. What is the proportion of the circle diameter a to the line segment b?
Scroll down for a solution to this problem.
Solution
The proportion a : b is √2 : 1.
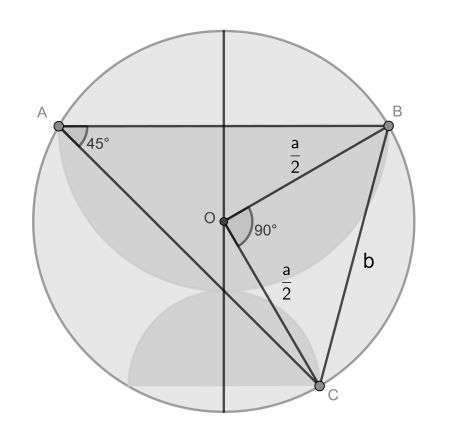
First, draw the line segments AB and AC. The first is the diameter of the larger semicircle, whereas the latter goes through the touchpoint. Therefore, they have an angle of 45°.
Now use the Inscribed angle theorem to infer that the angel BOC at the circle centre is 90°. Then it is simply a matter applying the Pythagorean theorem to find that b=a/√2.
Poem
This problem inspired Belladonna to the following poem:
Le gobelet de feu
Pour certains
Pour d’autres un calice
Ouvert pour recevoir
Les abeilles qui butinent
Où le vase sacré du ciboire
Un creuset qui accueille
Les biens terrestres
Les formes généreuses
Une coupe heureuse
Belladonna