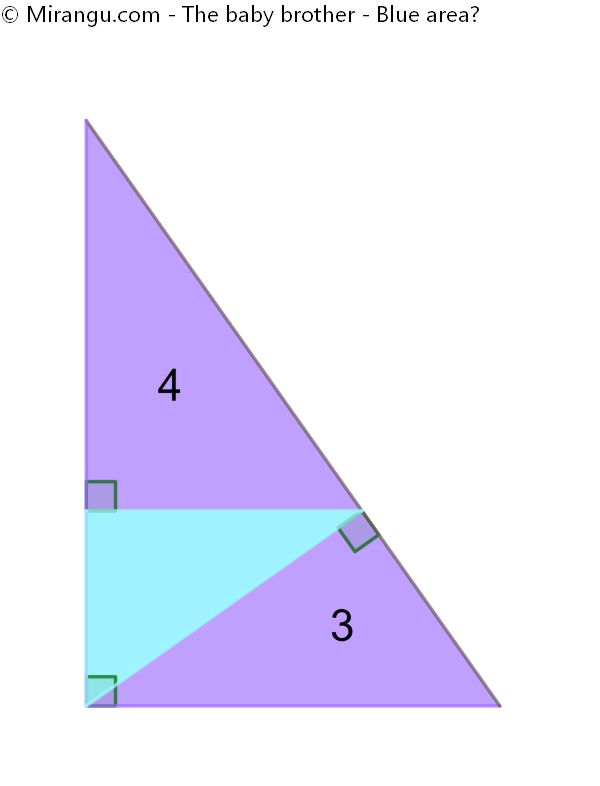
Three small right triangles embedded in a large right triangle. Two of the areas are given. What’s the area of the smallest one?

Solution

The blue area is 2.

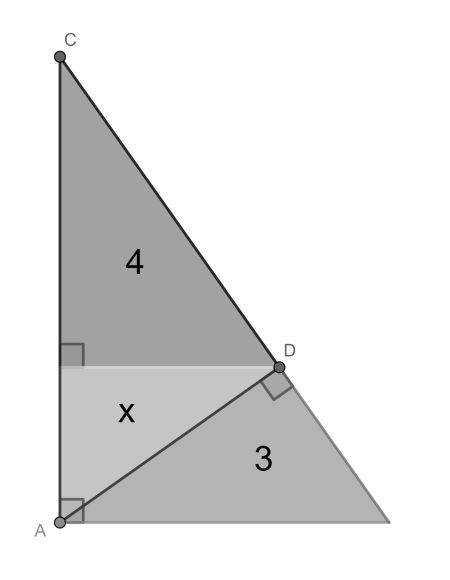
The solution hinges on the use of similarity. There are five similar right triangles in the diagram. The three small ones, the largest one, but also triangle ADC.

This latter triangle is divided by the altitude on the hypotenuse, just like the largest one. Therefore we can equate the area proportion of their parts, so x : 4 = 3 : x+4. This gives the quadratic equation x²+4x-12=0, which has roots -6 and 2. Disregarding the negative root, we arrive at the answer.