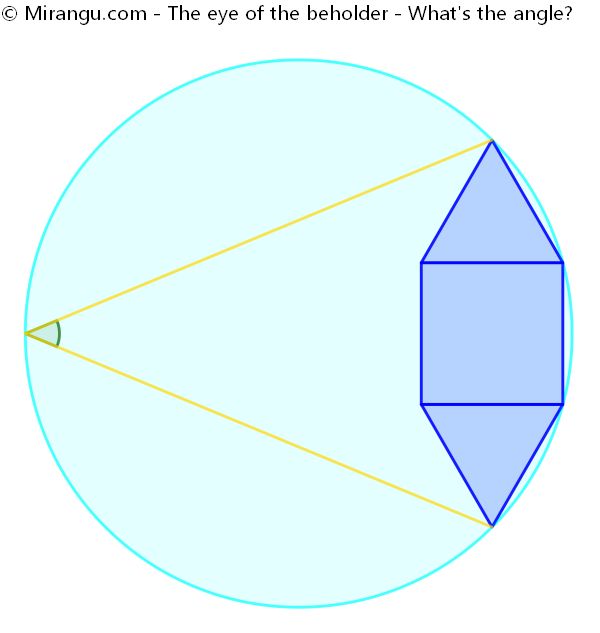
A square and two equilateral triangles inside and touching a circle. What’s the angle α?
Scroll down for a solution to this problem.
Solution
The angle is 45°.
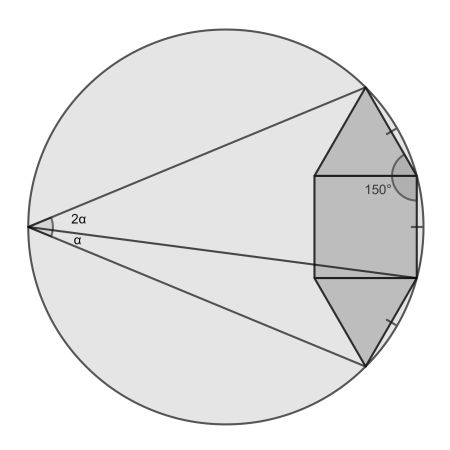
This solution was provided by Eylem Gercek Boss.
The first ingredient is the observation that the three marked chords are equal and thus span equal angles at the centre, and due to the Inscribed angle theorem also at the circumference. Therefore the requested angle can be divided into α and 2α as shown.
Next acknowledge that the 2α is part of a cyclic quadrilateral, and therefore must be 180° minus the opposing angle. This is 150°, so α must be 15°.
Poem
Inspired by The eye of the beholder, geometrical poet Belladonna composed the following poem:
Le diamant bleu est enfermé
Et son regard a transpercé
D’un rayon jaune lumineux
Ce beau coffre si précieux.
Le diamant, pierre éternelle
A offrir pour l’amour de sa belle
Il va encore plus scintiller
Et de mille feux toujours briller .
Belladonna