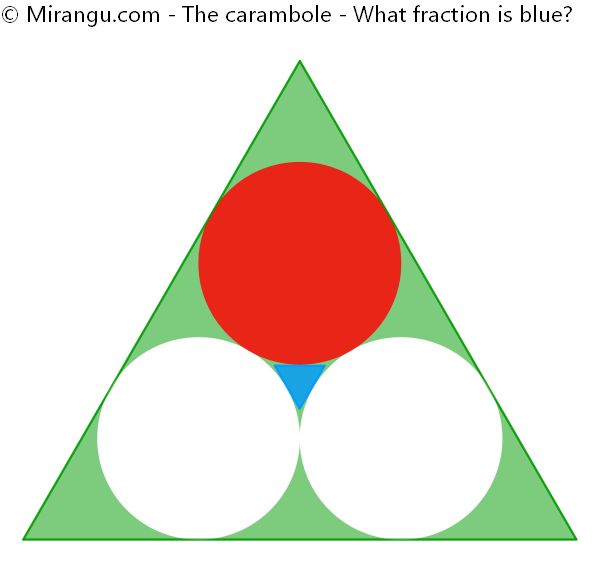
Three touching congruent circles inscribed in an equilateral triangle. A small equilateral triangle inscribed in the centre space. What fraction is blue?
Scroll down for a solution to this problem.
Solution
The blue triangle covers 13-15√3/2 of the large triangle, which is approximately 0,96%.
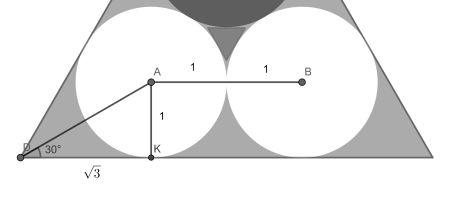
Let’s assume that the circles have radius 1. From the figure above it is straightforward that the side a of the large triangle is a=2+2√3.
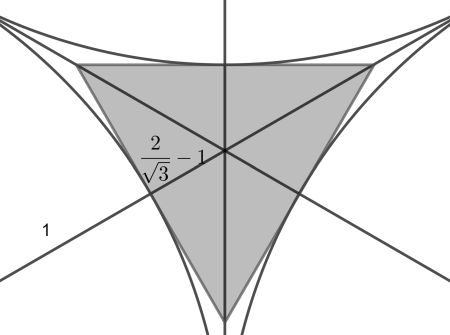
The centres of the three circles also form an equilateral triangle with side 2. It is concentric with the blue triangle. Now the distance of a vertex of this triangle to the common centre is 2/√3.
Now we can use this to find the side length b of the smallest triangle. It is 2√3 times the distance from a side to the centre, which is 2/√3-1. This gives b=4-2√3. The required fraction is the square of b/a.
Poem
We thank geometric poet Belladonna for the following apt poem:
La carambole ou pomme de goa la bien nommée
A dans son coeur en étoile
Une carpelle qu’elle dévoile
On y trouve la vie qu’elle recèle
Elle s’offre délicieuse
Fruit en fleur précieuse
Offerte en porte bonheur au nouvel an
Elle ravit petits et grands gourmands