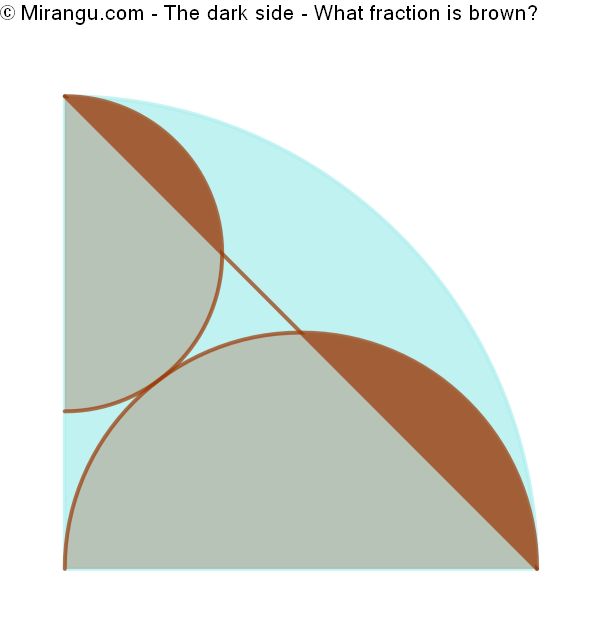
A quarter circle containing two touching semicircles cut by a chord. What fraction is brown?
Scroll down for a solution to this problem.
Solution
A fraction of 13/36*(1-2/pi) is brown, which is approximately 0,13.
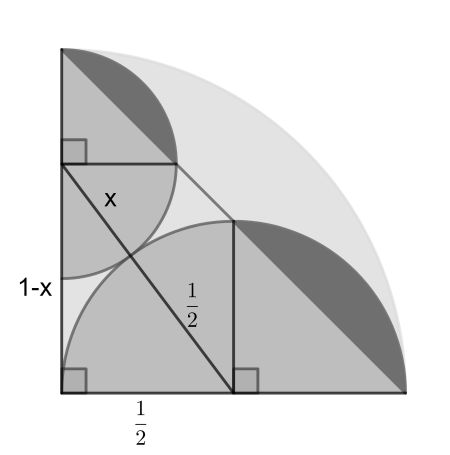
The first part of the solution is to find the radii of the semicircles. Setting the radius of the quarter circle to 1, the larger semicircle has 1/2. From the right triangle in the centre and the Pythagorean theorem we get for the smaller one x=1/3.
The next step is to recognize that the brown circular segments are similar to each other and to the one of the quarter circle spanning 90°. This is due to the fact that the three circles touch each other and the chord is passing through the tangency points.
Now a 90° circular segment has area r2(π-2)/4. Thus, we get for the brown area (1/4+1/9)*(π-2)/4. Dividing this by the total area π/4 we arrive at the required fraction.
Poem
Geometrical poet Belladonna associated freely on The dark side:
Le soleil est éclipsé
Par la lune
Le coeur est affamé
Vidé le sourire
Aucune peur de mourir
Dans Starwars et sa guerre
On sabote
L’étoile au super laser
Planète stellaire détruite
Aussitôt reconstruite
Dans la lune forestière
Bella