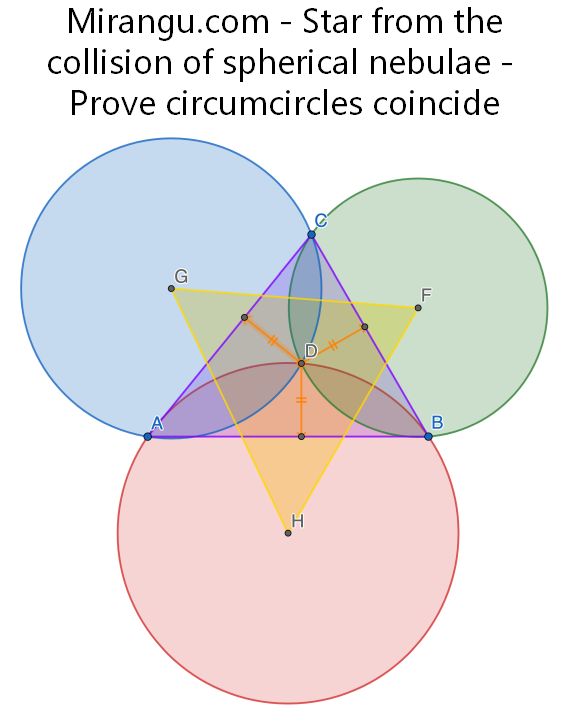
From the purple triangle ABC and the center of its inscribed circle at D, form the three colored circles (BDC), (CDA), and (ADB), with centers F, G, H, respectively, thus forming the yellow triangle FGH.  Prove that there is one circle that circumscribes both triangles.

Solution

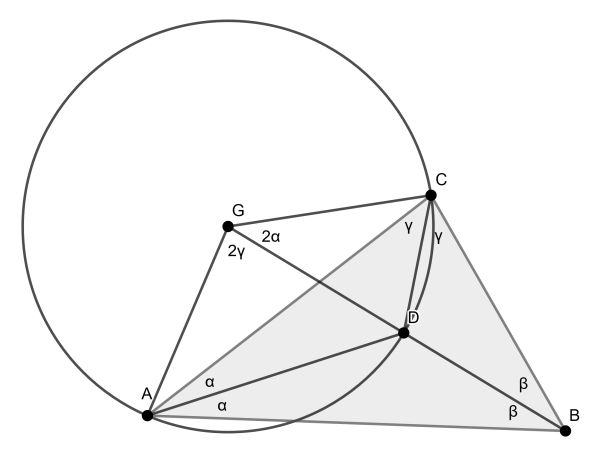
Focus on the blue circle first. Since D is the incentre of triangle ABC, it bisects its angles. Using the inscribed angle theorem, we get the angles as shown above.

Now ∠AGC=2(α+γ)=180-2β=180-∠ABC. So ABCG is cyclic. Similarly we can show that AHBC and ABFC are cyclic, implying that AHBFCG is cyclic.

From the purple triangle ABC and the center of its inscribed circle at D, form the three colored circles (BDC), (CDA), and (ADB), with centers F, G, H, thus forming the yellow triangle FGH.  Prove that there is one circle that circumscribes both triangles. By @MarshallWBuck pic.twitter.com/IWvlowuKED

— Mirangu (@Mirangu1) April 14, 2023