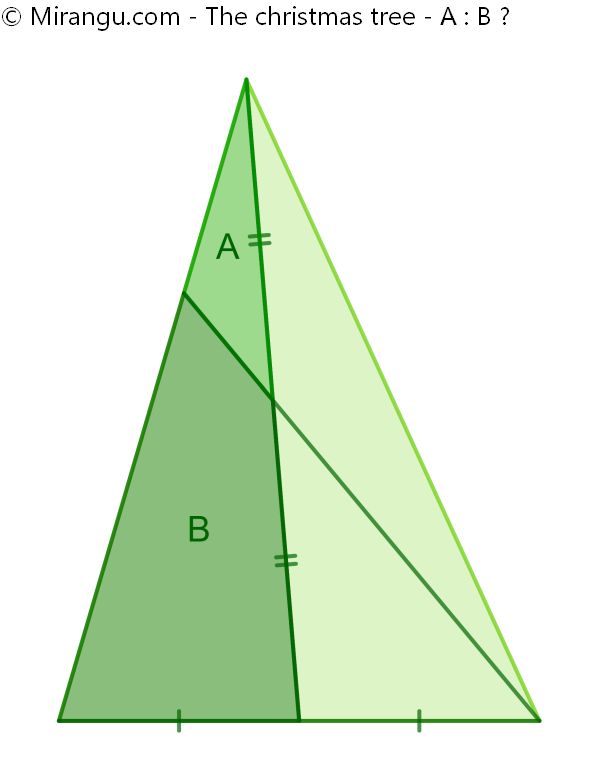
A triangle, a median and another cevian. What is the proportion of the two areas?
Scroll down for a solution to this problem.
Solution
The proportion A : B is 1 : 5.
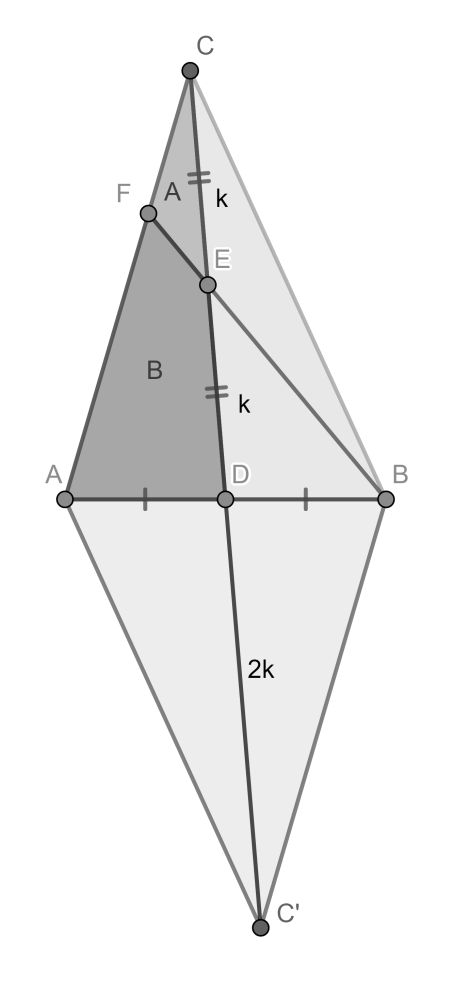
The crucial part of the proof is to find the proportion of segment CF to CA. It follows from doubling the triangle as shown, forming a parallelogram. Comparing triangles CFE and C’BE it is readily seen they are similar. From CE : EC’ is 1 : 3 and because CA=BC’ it follows that CF : CA = 1 : 3.
Comparing triangles CAD and CFE, they have the same top angle and their adjacent sides have proportion 3 and 2 respectively. Hence A+B=6A, so B=5A.
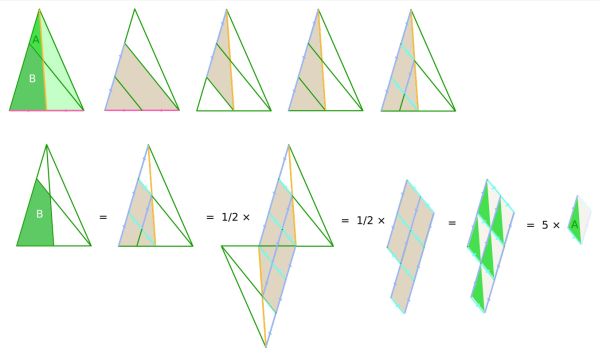
Visual solution
Geometrical artist David Andriana provided the follow purely visual proof for The christmas tree:
Poem
Geometrical poet Belladonna crafted this poem for the occasion:
24 décembre 2020
C’est Noël ce soir
Un jour plein d’espoir
Grâce au roi de la forêt
Pour y croire
Arbre royal mon beau sapin
Tu connais tant d’histoires
Tu sais les malheurs,
Les joies et les pleurs
Tu réconfortes les coeurs
Tu es notre porte-bonheur
Belladonna