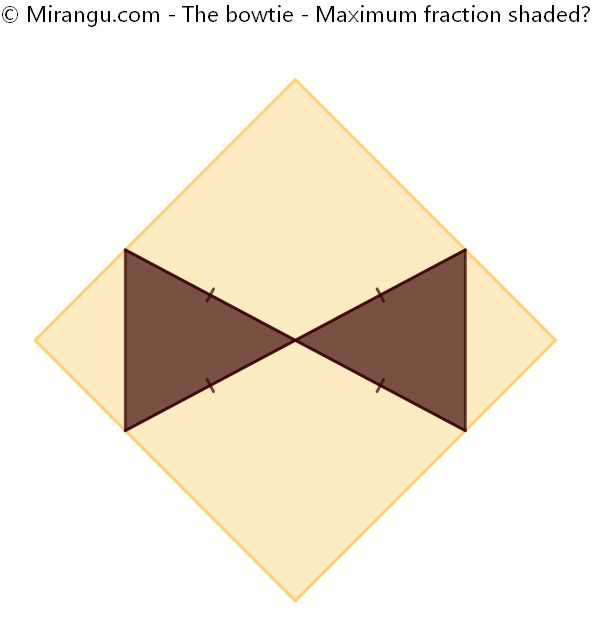
A square and two congruent isosceles triangles with variable top angle. What is the maximum fraction shaded?
Scroll down for a solution to this problem.
Solution
A maximum of 1/4 is shaded.
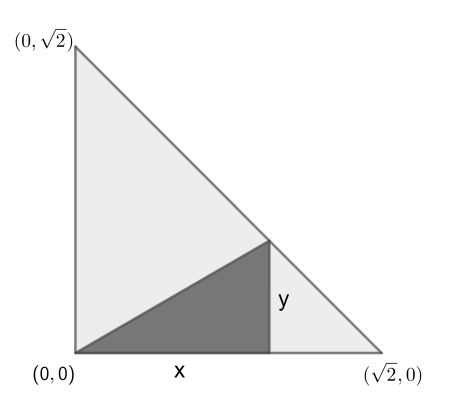
First, acknowledge that the figure has reflection symmetry in both diagonals, so we can limit ourselves to a single quadrant. Choose the short sides of this 45-45-90 triangle to be √2, such that its area is 1.
The required fraction can then be written as xy/2. Since y is on the hypotenuse, it can be expressed as y=√2-x and the fraction A(x)=x(√2-x)/2.
To find the maximum, set the derivative with respect to x to 0. So A'(x)=√2/2-x=0. One finds x=√2/2, which is exactly halfway the side. The corresponding fraction is 1/4.