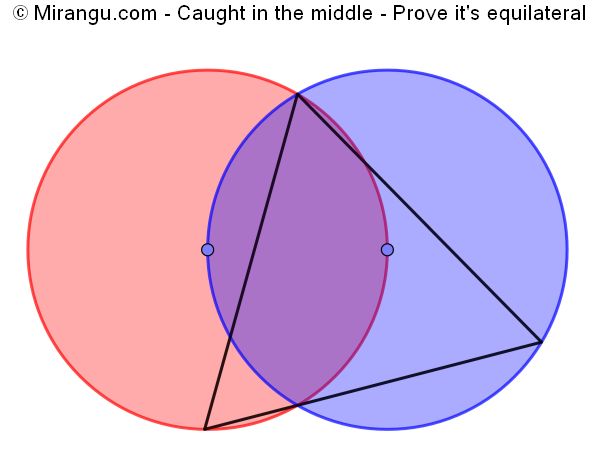
Two circles support a triangle. Prove it is equilateral.

Solution

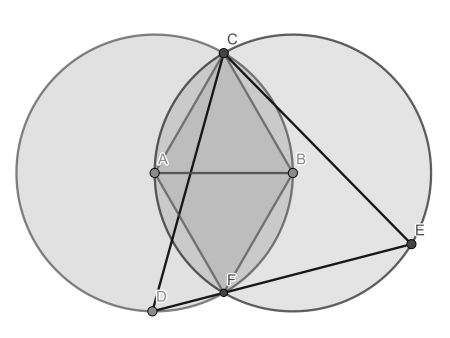
The proof follows these steps:

1. Because AB is a radius of both circles, they are congruent.
2. Inspection of the sides of triangles ABC and ABF reveals they are both equilateral.
3. The angle at the centre FAC is therefore 120°.
4. Using the Inscribed angle theorem, it follows that angle FDC is 60°.
5. Similarly angle FEC is 60°.
6. Using the interior angle sum, also angle DCE is 60°, so all three angles of triangle DEC are equal.

Please look here for a nice animation of this puzzle by Ignacio Larrosa Cañestro.

Poem

Where is our place ?
In the middle of what ?
The earth in the Cosmos, in the Universe?
But we are not the center
Passing through the Milky Way
What is Universe ?
Finished or Infinite
But we know
We are in the middle of our feelings, living and dying
One day !

Bella

Poem 2

Feeling
Balancing
Coming
And
Going
Dancing
With
Soul and
Heart
And
Spirit
A caress
With tenderness

Bella