Two isosceles triangles are placed as shown. What is the proportion of the line segments a and b?
Scroll down for a solution to this problem.
Solution
The proportion a : b is 1 : 2.
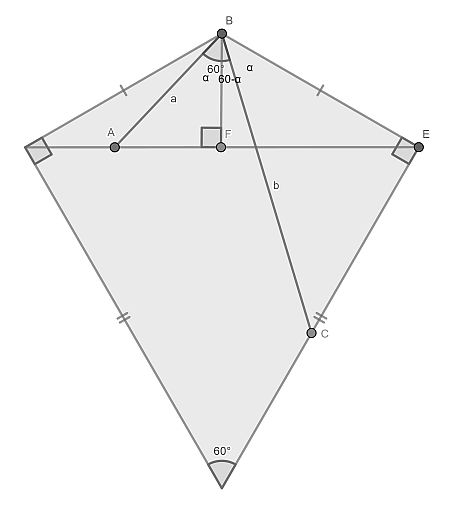
First draw the altitude BF from the top vertex. It is easy to see that triangle BFE is a right triangle with 60° in the top vertex.
Now compare right triangles AFB and CEB. They have the same angle α en hence they are similar.
Now from the 30-60-90 triangle BFE it is seen that BF : BE = 1 : 2. Therefore also the hypotenuses a : b = 1 : 2.
Note 1: triangle ABC also is a 30-60-90 triangle; one of the many in this interesting figure.
Note 2: all possible configurations are dynamically shown in this beautiful animation by Ignacio Larrosa Cañestro.
2 replies on “The blue diamond”
Los vértices superior y derecho del diamante y los otros extremos de los segmentoa a y b son concíclicos, pues el segmento que une estos extremos se ve bajo un ángulo de 60º desde los dos vértices. Como uno de los ángulos del cuadrilátero inscrito resultante es recto, también lo es su opuesto, y b y a son la hipotenusa y el catto de un triángulo rectángulos 30º-60º-90º, por lo que b=2a
https://twitter.com/Mirangu1/status/1328975603945639936?s=20
Senor, my Spanish is not quite sufficient to follow your proof, but I have the fullest confidence in its validity.