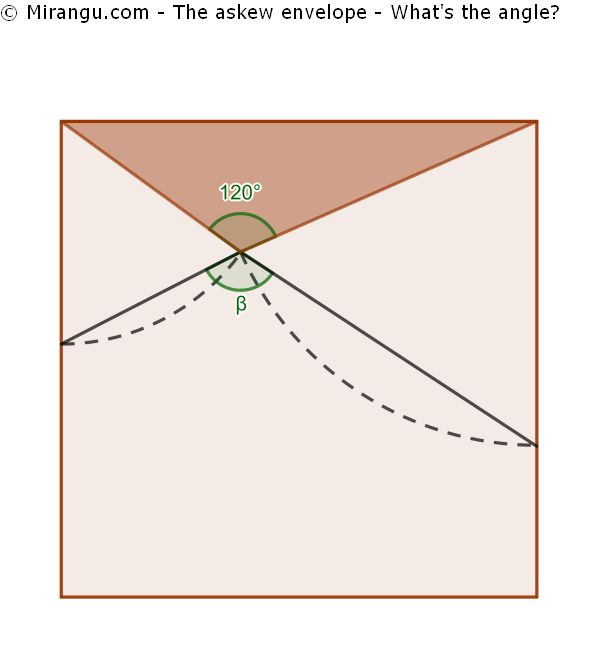
In a square, an interior point is drawn with an angle to the top vertices of 120°. What’s the angle between the chords formed by the two arcs centered in these vertices?
Scroll down for a solution to this problem.
Solution
The angle β is also 120°.
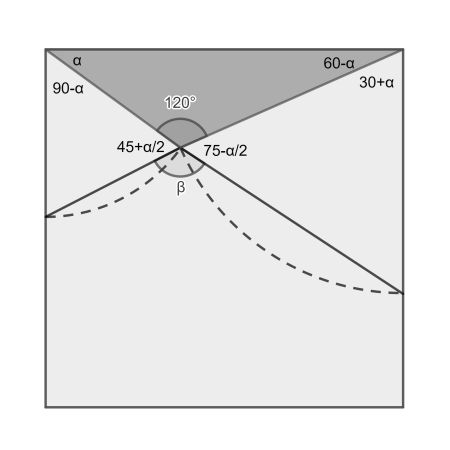
The solution follows from straightforward angle propagation. Start with α in the right corner of the dark triangle. Use the fact that:
- angles in a triangle add up to 180
- the chord triangles are both isosceles
- the two bottom angles in an isosceles triangle are equal
Now β=360-120-(45+α/2)-(75-α/2)=120.