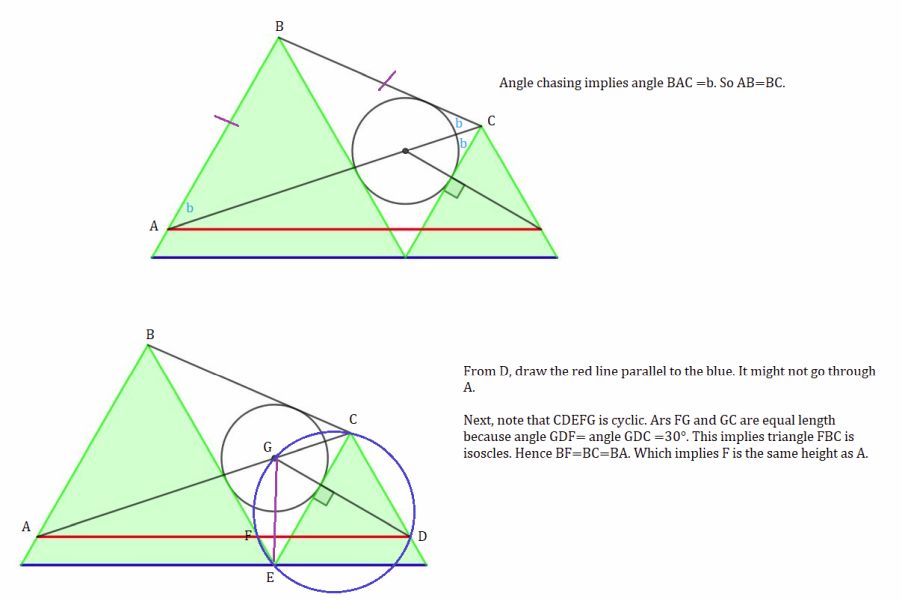
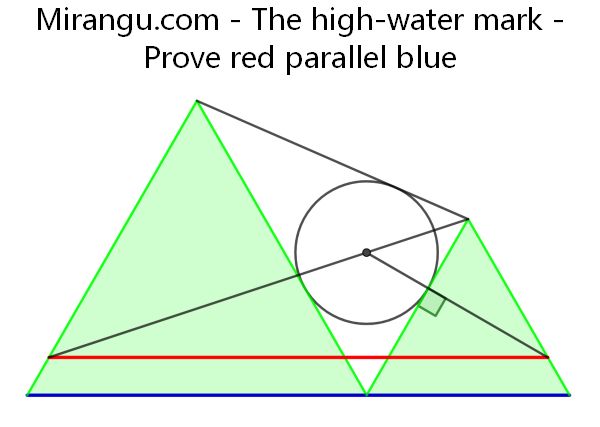
Two equilateral triangles on a blue line segment. Prove that the red line segment is parallel to it.
Scroll down for a solution to this problem.
Solution
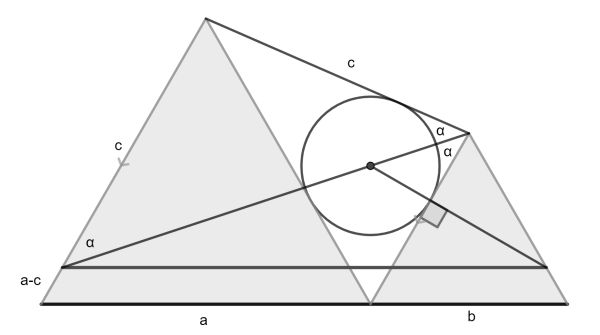
Start with the left side of the diagram. One discerns an isosceles triangle, because of the angle bisector and because the left sides of the equilateral triangles are parallel. The distance from the left side of the red line segment to the blue one is seen to be a-c.
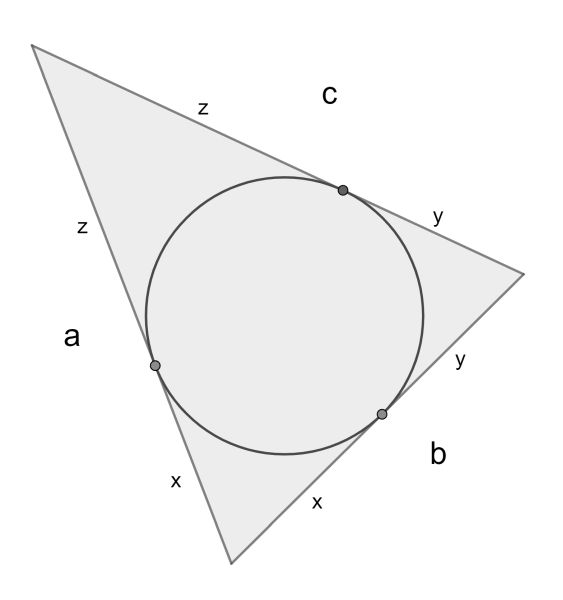
For the right side, we use a lemma relating the distances from the tangency points of the incircle to the vertices to the side lengths. We have a=x+z, b=x+y and c=y+z. This leads to x=(a+b-c)/2, y=(-a+b+c)/2 and z=(a-b+c)/2.
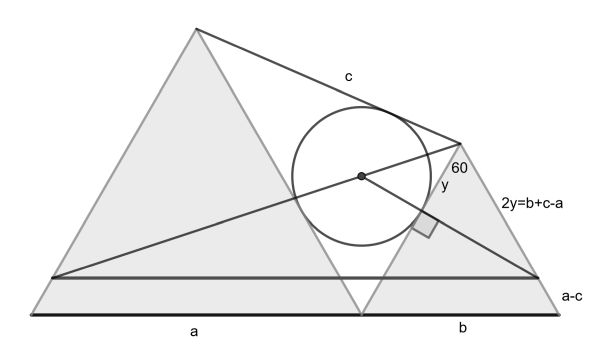
Now using the 30-60-90 triangle on the right, we get that the right height of the red segment is also a-c. Therefore blue and red are parallel.