A square contains a red rectangle with an extended side. Prove that red=|AB||AC|+|BE||CD|. By Matthew Arcus.
Squaring a rectangle II
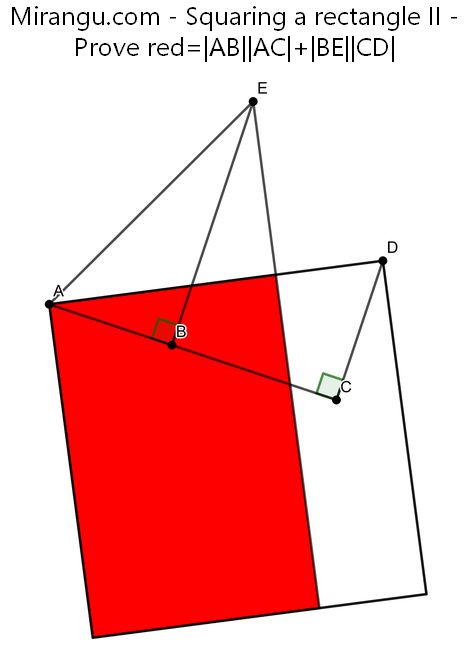

A square contains a red rectangle with an extended side. Prove that red=|AB||AC|+|BE||CD|. By Matthew Arcus.
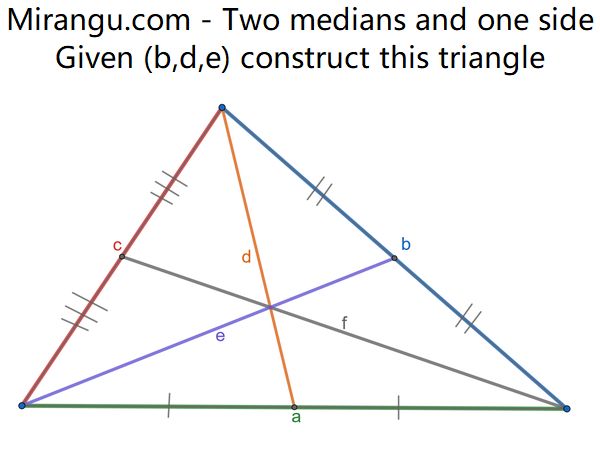
A triangle has sides a,b,c and the medians d,e,f ending at those sides, respectively. Given only the lengths (b,d,e) construct the triangle (a,b,c). (Start with a triangle with side lengths determined in some manor from the given 3 lengths.)
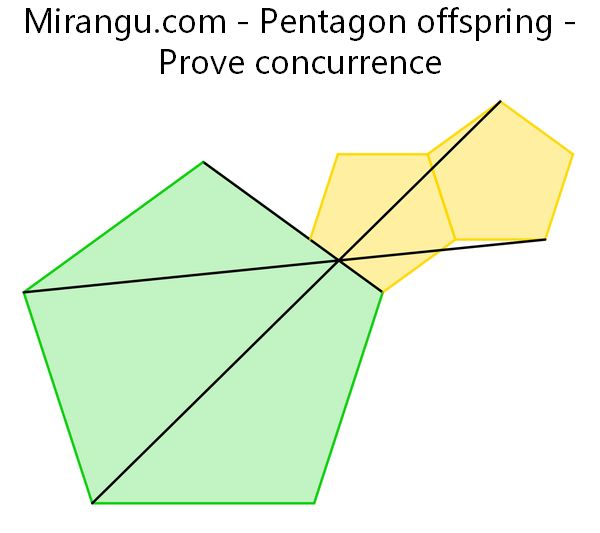
Three regular pentagons are placed as shown. Prove that the three black line segments are concurrent.
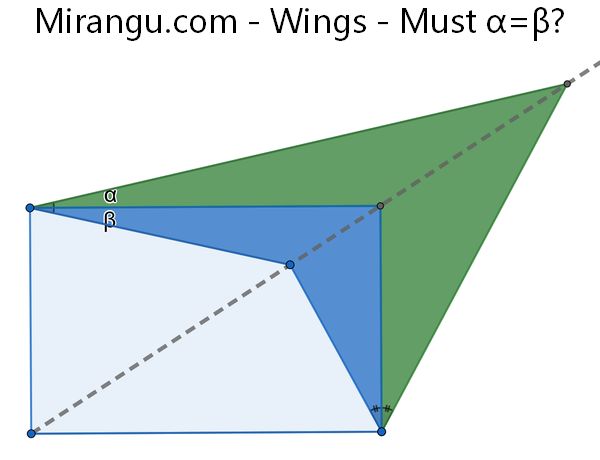
Two wings are attached to the corner of a rectangle, and have corners lined up with the diagonal of the rectangle. The angles at the lower wing tips are equal. Must α = β at the left wing tips?
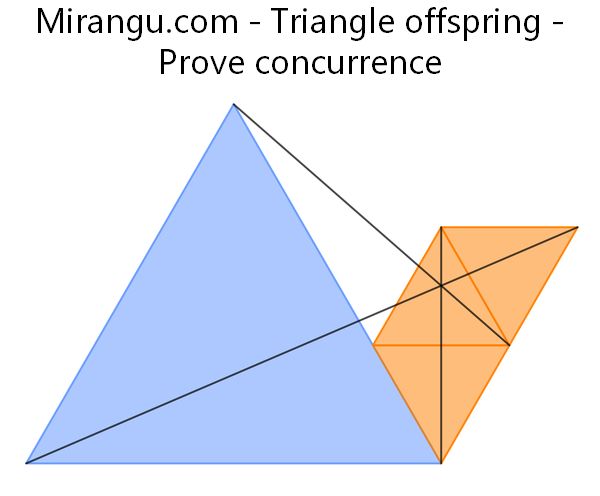
Four equilateral triangles. Prove that the three black line segments are concurrent.
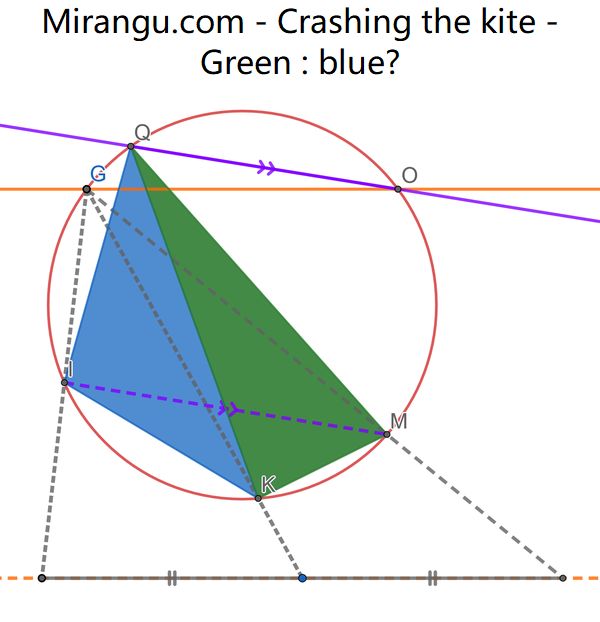
The orange lines are parallel, the purple lines are parallel, the dotted gray lines intersect the base at equal distances. What is the ratio of areas of the blue and green triangles?
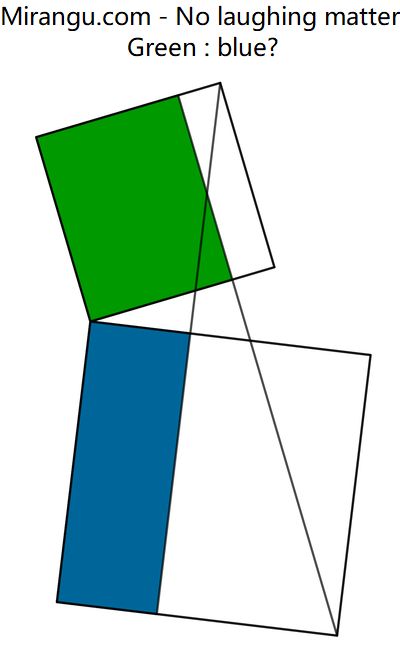
Two squares share a vertex. Each square contains a coloured rectangle with extended side. What’s green : blue? By Matthew Arcus.
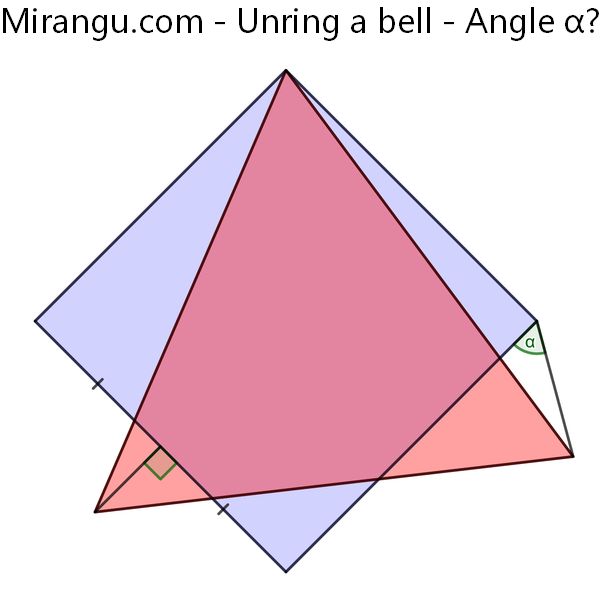
A square and an equilateral triangle. What’s the angle α?
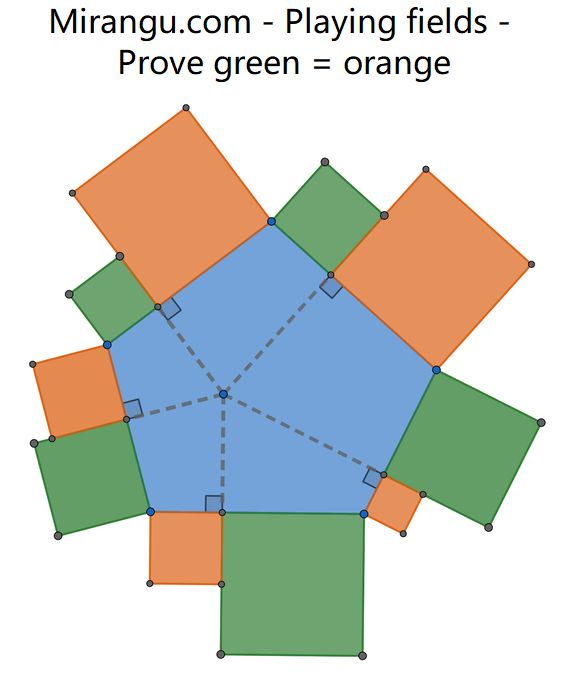
Show equality of the green and orange square playing field areas.
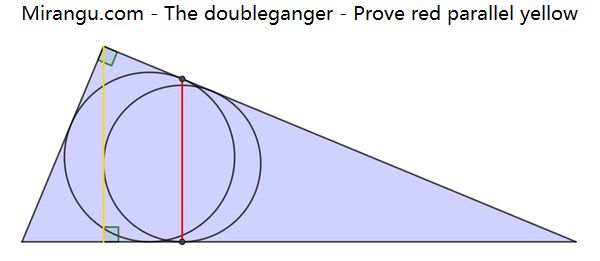
Two nested right triangles with their incircles. Two tangency points are shown. Prove that the red and yellow line segments are parallel.
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now