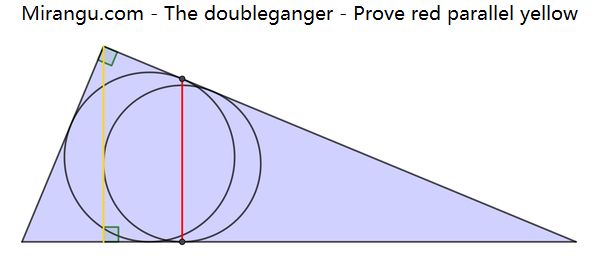
Two nested right triangles with their incircles. Two tangency points are shown. Prove that the red and yellow line segments are parallel.
Scroll down for a solution to this problem.
Solution
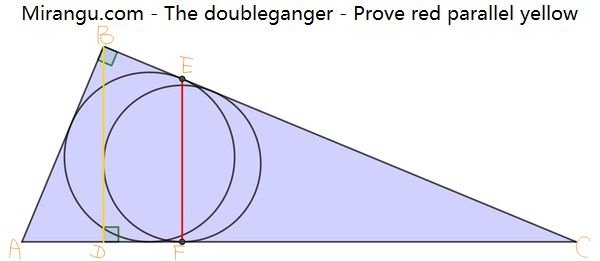
The argument is that triangle ABC with its incircle is similar to triangle BDC with its incircle. This implies that |CE| : |CB| = |CF| : |CD|, which, by the converse of the Triangle proportionality theorem, ensures that BD // EF.
Video
Please find here the video solution: Video: The doubleganger.