Four squares and five shared vertices. If the orange area is 4, what is the green area?
The dangling square
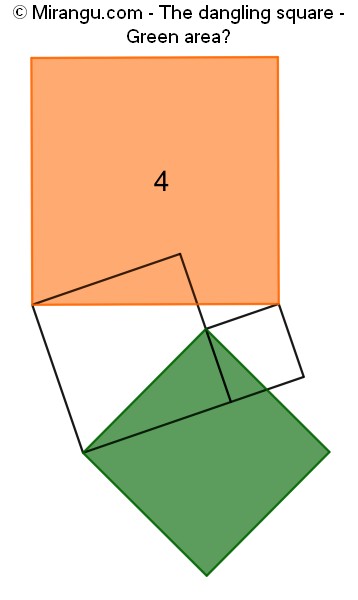

Four squares and five shared vertices. If the orange area is 4, what is the green area?
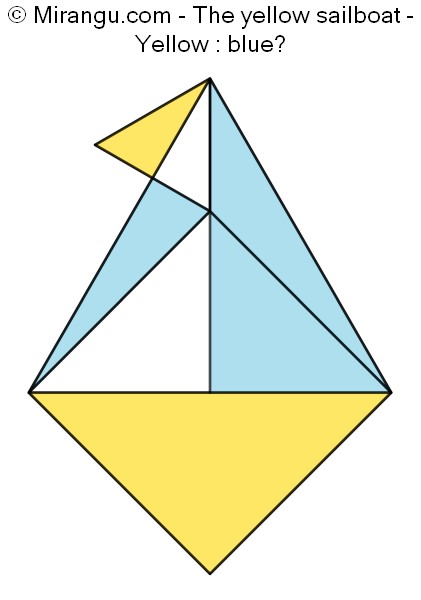
A square, two equilateral triangles and an extended side. What is the proportion yellow : blue?

A square contains three squares (black sides), one of which has an extended side (blue). What is the proportion yellow : blue?
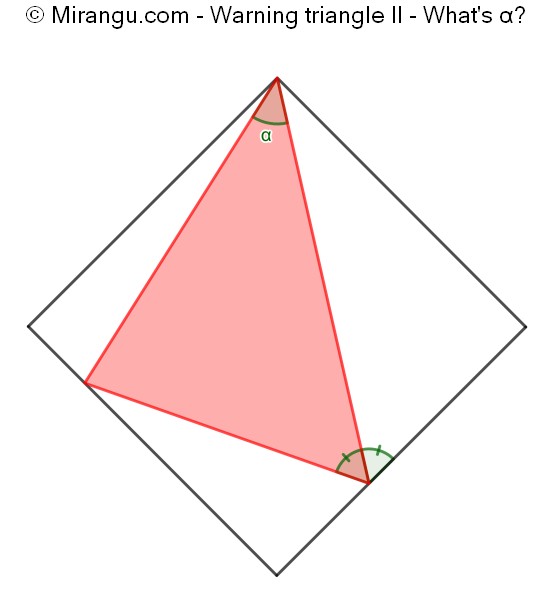
A square, a triangle and two equal angles. What is the angle α?
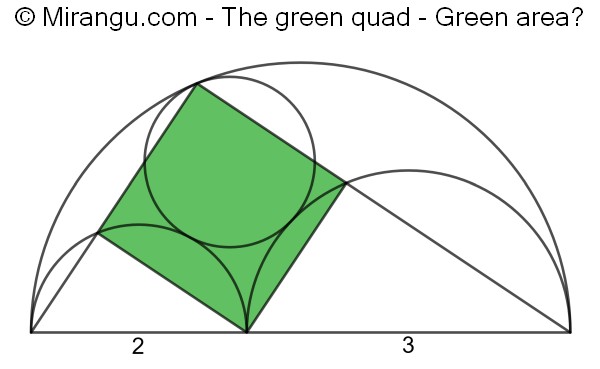
Three semicircles and a circle all touching each other. The diameters of the two smallest semicircles are given. The large triangle connects three tangency points. What is the area of the green quadrilateral?
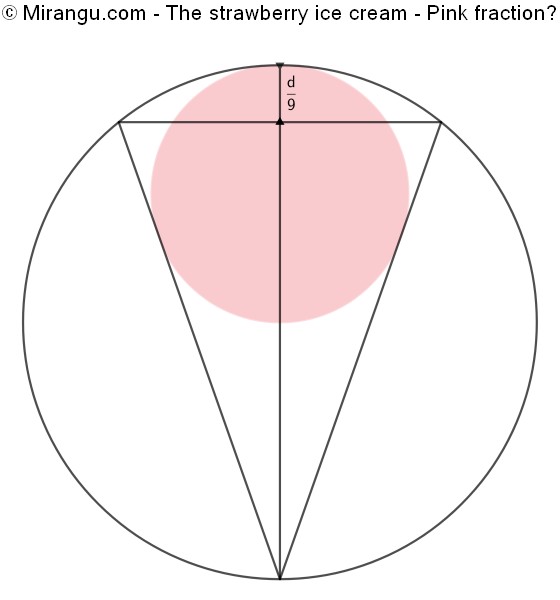
Two tangent circles and a triangle. The figure has reflection symmetry in the vertical diameter d, of which one ninth is above the horizontal chord. What fraction is pink?
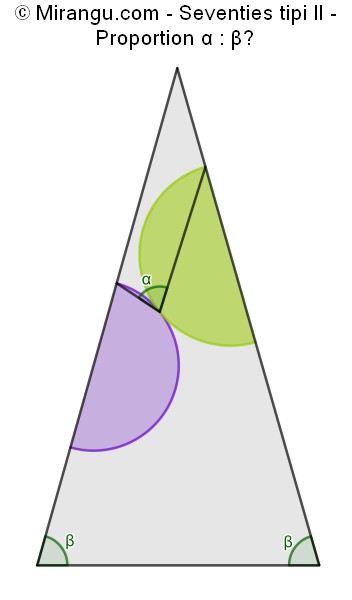
A triangle containing two tangent semicircles. What’s the proportion α : β?
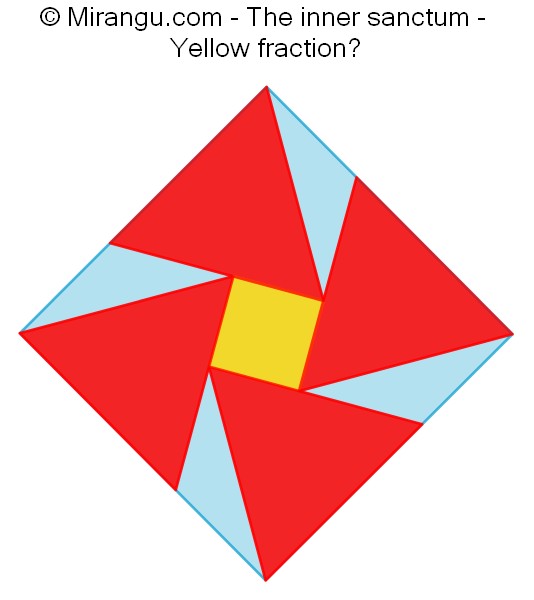
A square with four congruent equilateral triangles. What fraction is yellow?
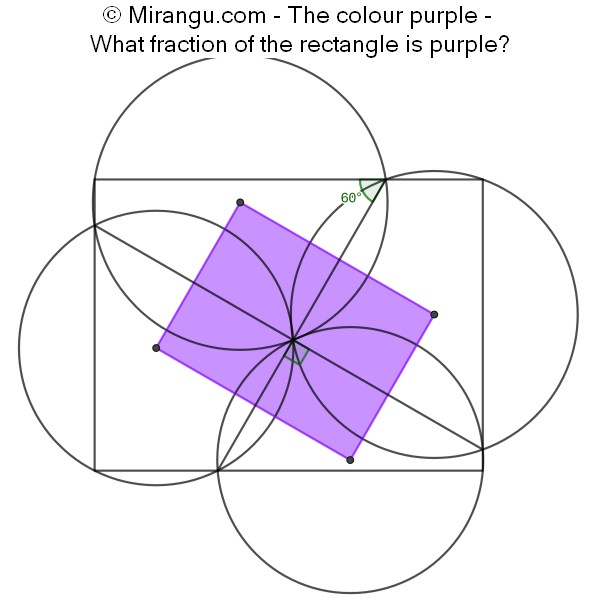
A rectangle is split by two perpendicular lines. The four circles pass through vertices and intersection points. Their centres form a purple quadrilateral. What fraction of the large rectangle area does it cover?
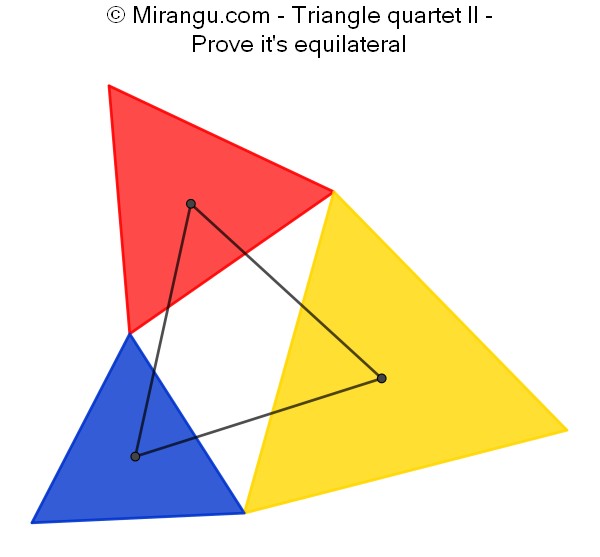
Three coloured equilateral triangles share three vertices. Prove that the triangle formed by their centres is also equilateral.1This puzzle is also known as Napoleon’s Theorem.