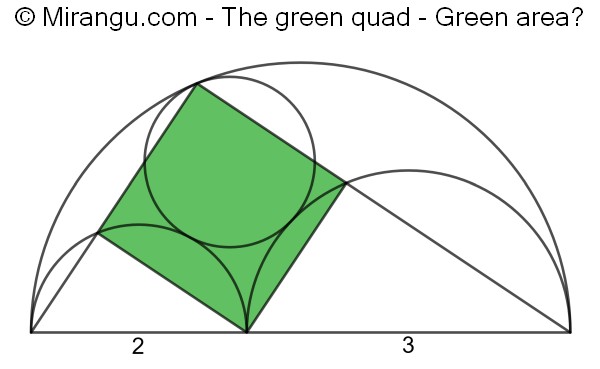
Three semicircles and a circle all touching each other. The diameters of the two smallest semicircles are given. The large triangle connects three tangency points. What is the area of the green quadrilateral?
Scroll down for a solution to this problem.
Solution
The green quadrilateral is a square with area 36/13.

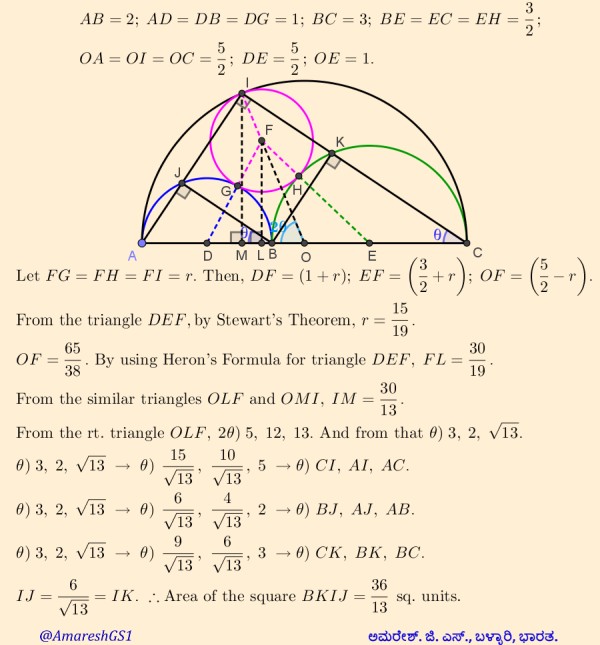
2 replies on “The green quad”
The diagram is basically that in Archimedes’ “Book of Lemmas”, Proposition 6, where the author proves that the quadrilateral is a rectangle, but does not point out that it is really a square. The purpose of his Proposition 6 is to arrive at the formula for the radius r of the inscribed circle in terms of the radii a, b of the small semicircles. Archimedes finds r= ab(a+b)/(a^2+ab+b^2).
A modern proof of Archimedes’ result would use the law of cosines twice, as in Peter Gallin’s solution above, and would find that Cosine(alpha) =
(a^2-b^2)/(a^2+b^2), giving 2a(a+b)/sqrt(a^2+b^2) for the left side length of the big right triangle, and 2b(a+b)/sqrt(a^2+b^2) for the right side length. The ration a:b for these side lengths easily translates (using similarity of all the right triangles) to a ratio 1:1 for the side lengths of the rectangle/square in question.
A natural question to ask: is there a simple direct proof of the square property that avoids the algebra needed to determine the formula for the cosine of alpha?
Since the procedure to construct the diagram is left-right symmetrical, so must be the ratio of green rectangle sides. It can only be 1, otherwise one would be able discern a preferred side.