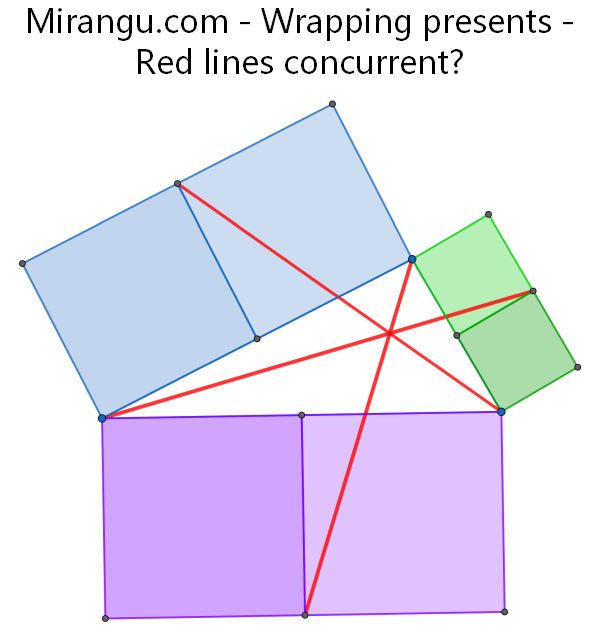
Six squares are wrapped together with red ribbons. Do they cross at a single point?

Solution

Yes, the red lines are concurrent.

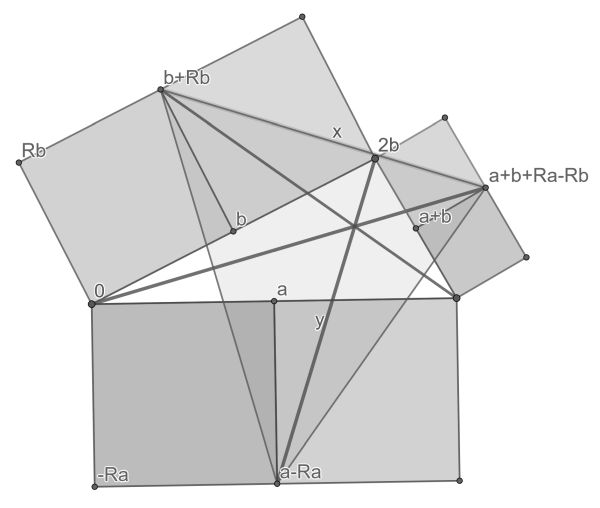
Choose the origin as shown in the figure. The vertices denote the ends of vectors. R is an anticlockwise rotation over 90°.

Now vector x=a+b+Ra-Rb-(b+Rb)=a+Ra-2Rb, whereas vector y=2b-(a-Ra)=2b–a+Ra. Applying R to x, and using the fact that R²=-1, you get Rx=Ra+R²a-2R²b=Ra–a+2b=y.

So y is the rotated x, i.e. it has equal length and is perpendicular to it. We conclude that the red line segments are perpendicular to the sides of the denoted triangle and go through the opposite vertex and therefore they intersect in its orthocentre.

Six squares are wrapped together with red ribbons. Do they cross at a single point? https://t.co/4NfVRVtX5E By @MarshallWBuck pic.twitter.com/KSVJq6CMXj

— Mirangu (@Mirangu1) July 4, 2023