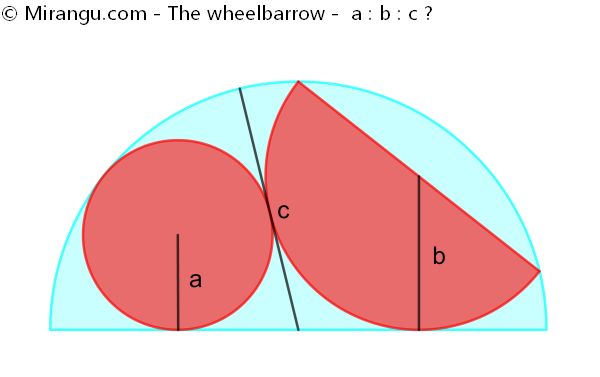
A circle and two semicircles are nested as shown. What’s the proportion of their respective radii a : b : c ?

Solution

The proportion a : b : c is 1 : φ : φ², where φ is the Golden Ratio.

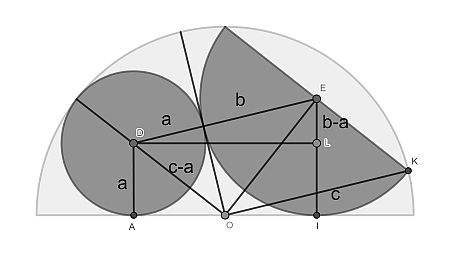
The strategy for the solution is to derive three expressions for the length of line segment AO, giving two equations one can solve.

The first expression comes from drawing the radius O through D and recognising that OD is c-a. Now from the right triangle OAD one gets |AO|²=c²-2ac.

For the second expression we use the fact that |AO|=|OI|, because O is a common point of three tangents and therefore the Tangent-tangent theorem can be applied twice. Now from right triangle OKE, one can derive that |OE|²=c²-b². Right triangle OIE then gives |AO|²=|OI|²=c²-2b².

The third expression for |AO| comes from right triangle DLE and the Pythagorean theorem. It gives |DL|²=4ab. Using again the fact that |AO|=|OI|, it follows that |AO|²=ab.

Now from equating c²-2ac, c²-2b² and ab, and setting a=1, one arrives at the desired solution.