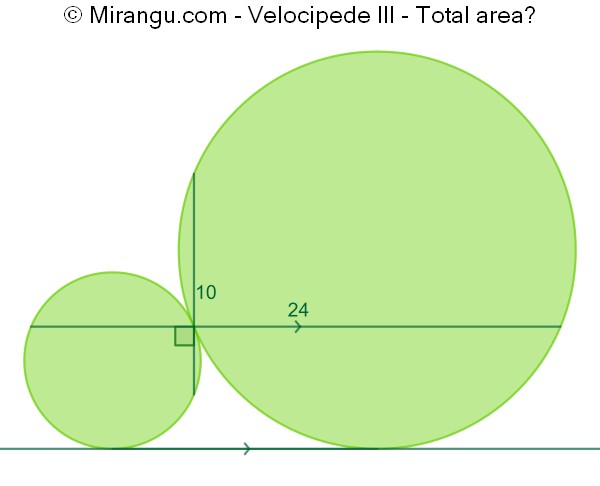
Two tangent circles and two line segments of given length crossing at right angles at the tangency point. One of the line segments is parallel to a common tangent. What’s the total area?
Scroll down for a solution to this problem.
Solution
The total area is 97π.
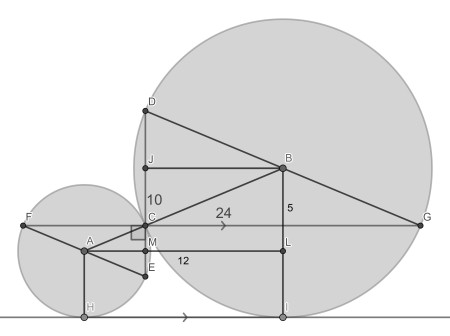
First draw a few parallel lines from the circle centres. Because of isosceles triangles we have that DJ equals JC and also CM equals ME. Therefore JM is half the total of 10, so the parallel line segment BL must be 5. Similarly, AL is seen to be 24/2=12.
Now if the small radius is r and the large circle has R, in right triangle ALB, the hypothenuse is R+r. We know from the Pythagorean theorem that R+r=√(122+52)=13.
Also from comparing AH and BI we have R-r=5. Combining the two gives r=4 and R=9. Hence the total area is (16+81)π.
Poem
The green velocipede
The two wheels rolls
They go on a trip
A journey full of mysteries
With his little brother
They believe in goodness and joy
The velocipede is like a toy
Both are tall
Just take care and don’t fall
Be carefull and don’t drive in a wall