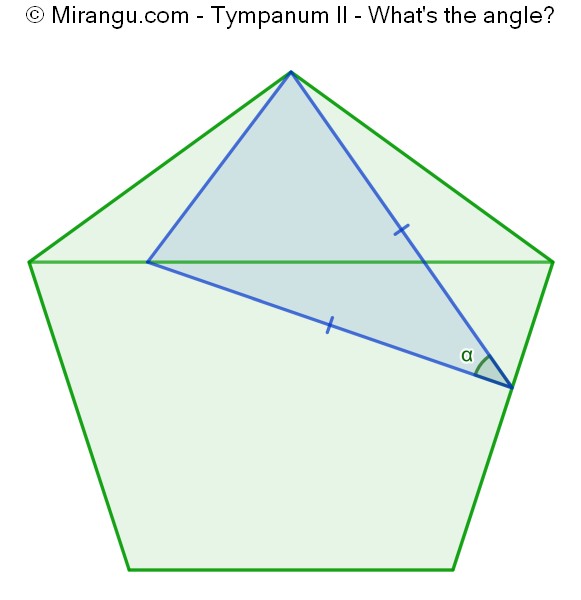
A regular pentagon with a diagonal. What is the top angle of the isosceles triangle?
Scroll down for a solution to this problem.
Solution
The angle α is 36°.
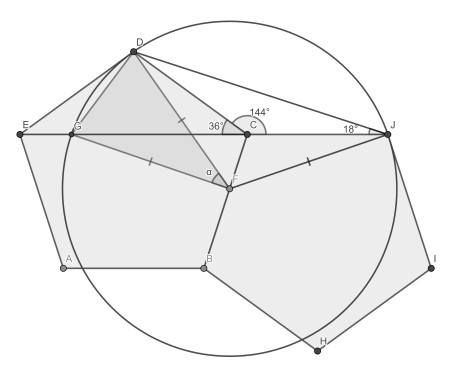
The crux of this solution is to mirror the pentagon in the side BC as shown. From reflection symmetry we deduce that |JF|=|DF|=|GF|. We can thus draw the circle through J, D and G with F as centre.
EJ is easily seen to be a straight line. Moreover, triangle DJC is isosceles with top angle 144°. Now, ∠GJD=∠CJD= 18°. From the inscribed angle theorem we get that α=36°.