Two congruent rectangles inscribed in a square. What fraction of the area is blue?

Solution

A fraction of 4-2√3 is blue. This is approximately 53,6%.

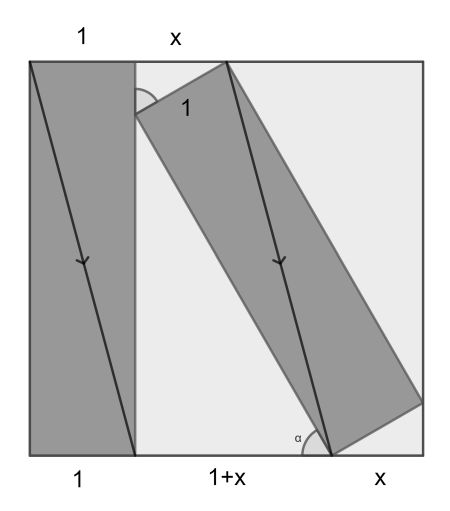
This solution starts by drawing the two congruent diagonals as shown. Since they span the same length, they must be parallel. If we set the rectangle short side to 1, we can fill in the lengths as shown.

Now since the square side length adds up to 2+2x, the cosine of angle α is 1/2 and therefore α is 60°. This we can use to find x in the similar little triangle: it must be x=√3/2.

The rectangles thus have total area 4(1+x), whereas the square has area 4(1+x)². The fraction is 1/(1+x)=4-2√3.

Poem

A hefty volume
Of informations
Of pictures production
Of a pandemic story
Of Covidie city
Of to much injury
Of hearts beating
Of doctors helping
Of people dying
Of helpers extraordinary
Of an humbling finality
Of a destruction from humanity

Bella