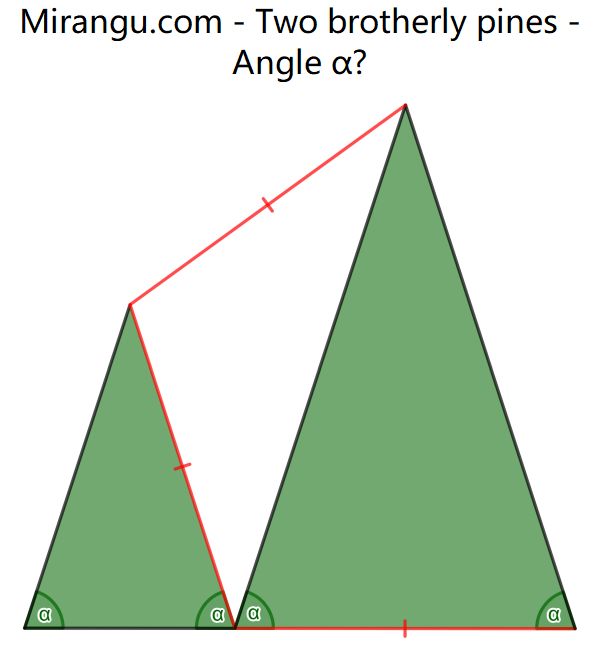
Three triangles are glued together. The green ones are based on a common line. What’s the angle α?
Scroll down for a solution to this problem.
Solution
The angle α is either 60° or 72°.
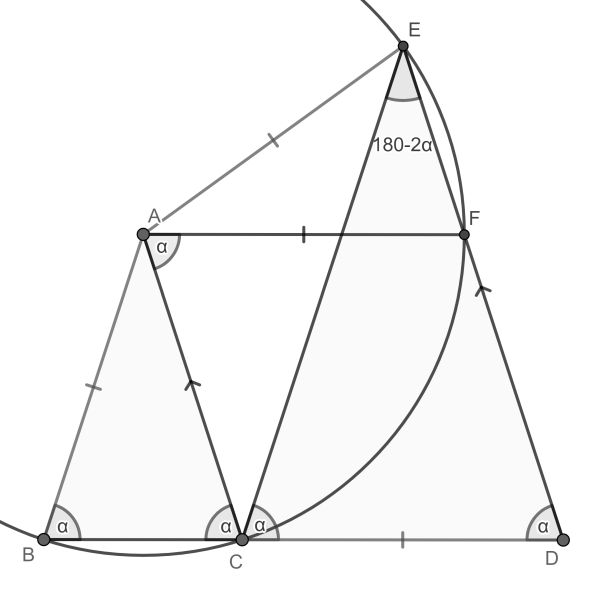
Start by acknowledging that sides AC and ED are parallel. One can therefore construct the parallelogram ACDF1Note that it is actually a rhombus.. Now draw the circle centred in A going through B, C, F and E. Using the Inscribed angle theorem, we have ∠CAF is twice ∠CEF. So α=2(180-2α), ergo α=72°.
It can, however, happen that AE is parallel to CD. The Inscribed angle theorem does not work anymore, since E and F coincide. In that case it is easily seen that all three triangles are equilateral and hence α=60°.
Poem
Two brotherly pines
Two green pines
Lived side by side
In beautiful brotherhood
Until the day
When the greatest
Was chosen
To decorate
The Xmas market
The little one cried and moaned
He refused
And wrapped their roots together
Thus
There were two trees
At the christmas market