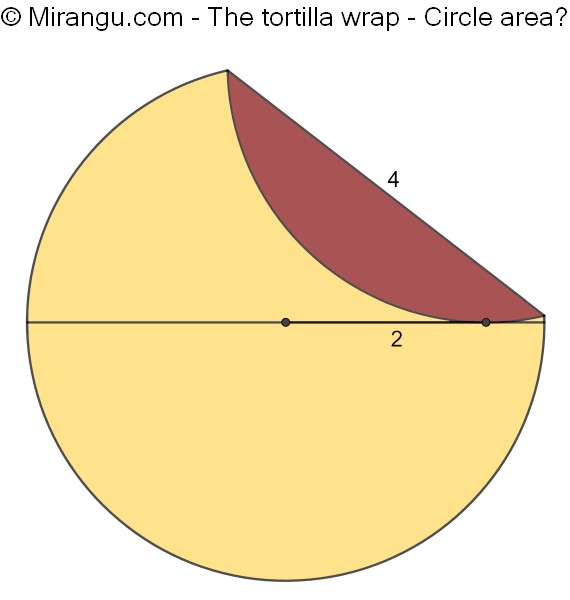
The edge of a circle is folded to touch a diameter. The tangency point lies 2 from the centre. Given that the fold has length 4, what was the circle area before folding?
Scroll down for a solution to this problem.
Solution
The circle area is 20π/3.
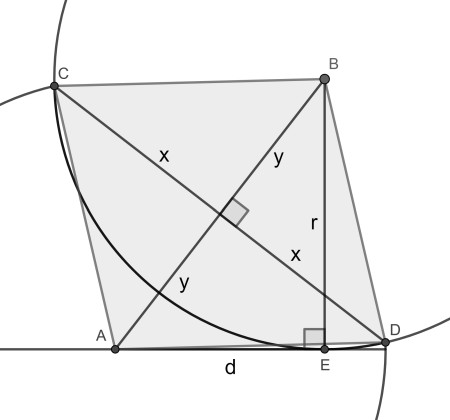
Let’s solve for the general case where the circle has radius r, the fold has length 2x and the distance centre to tangency point is d. Now the brown circular segment is part of a circle of equal radius r. The two centres and the intersection points form a rhombus with side r as shown.
Now, applying the Pythagorean theorem in triangle AEB gives 4y2=d2+r2. From the four congruent right triangles in the rhombus we have x2+y2=r2. Eliminating y from these two equations gives r2=(d2+4x2)/3. The answer comes from filling in d=2 and x=2.
Poem
The tortilla wraps
With whole wheat bread
A nice envelope to protect
Salmon, cheese or egg
A shelter packed UP in silver foil
With good food and not much oil
Tortillas wraps, sweet, salted or crispy
Filled with rice, beans, whatever you fancy
They look good and unify my family