Two touching circles, two diameters and two common tangents. What is the area of the green quadrilateral in terms of radii x and y?
Scroll down for a solution to this problem.
Solution
The green area is (x+y)√(xy).
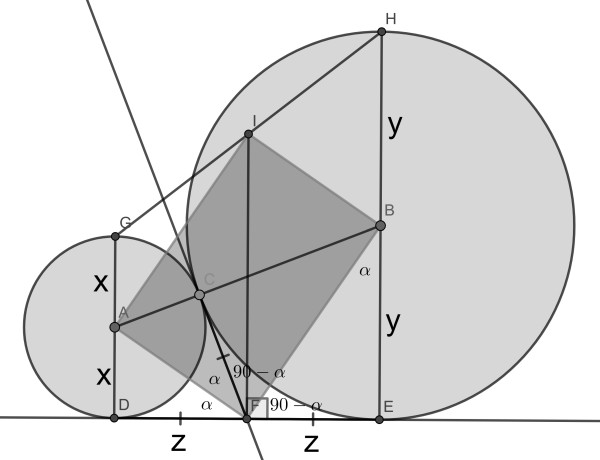
First, it is straightforward to establish that AFBI connects the midpoints of the quadrilateral DEHG. Now Varignon’s Theorem states that it must be a parallelogram. I thank Kamran Zamani for pointing this out to me.
Next consider the angles in F. It follows easily that angle AFB is straight, and hence AFBI is in fact a rectangle.
From similarity of triangles ADF and FEB it follows that z= √(xy) . Since the rectangle diagonals have length x+y, the green area follows.
Poem
The tipping point goes out to be
Like Omicron in Covidie
Like boiling water
Every day things are changing
And so the world goes on
Sharing confidence and sociability
“Silver tongue they’ll soon be gone
Will you ever know when it’s the tipping point”
(Tears for fears)

One reply on “The tipping point”
I feel inadequate to leave a reply to your excellent poetry and insight. Let it suffice to say that I’m humbled, proud and grateful to be mentioned here… 🙏😊