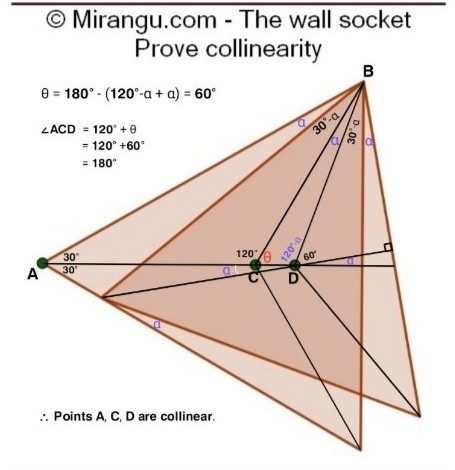
Two equilateral triangles share a vertex. Prove that their centres and the highlighted vertex are collinear.
Scroll down for a solution to this problem.
Solution
Poem
The wall socket
I’m the plug stuck in the wall
Open to all currents with everybody
I distribute the energy
I’m like magic
In this modern world
I’m always ready
Moving towards electricity
A miracle is happening
Out of the darkness coming
The light is sparkling
A sun is shining

3 replies on “The wall socket”
Orient the triangle and dilate so that in the complex plane the left-most green dot is the number 0 and the shared vertex is -w^2, where w is a 3rd root of unity. The second triangle has two vertices r and -w^2, where r is a real number. The third vertex is obtained by subtracting -w^2 from r, multiplying by w, and adding back to r, obtaining (r+w^2)w+r = (1+w)r+1. Sum of the three vertices is (1+w)r+1+r-w^2 = r(w+2) + (1-w^2) = (r+1)(1-w^2). The centroid of the other triangle is (1-w^2)/3, so both centroids are real multiplies of the same complex number, and thus on the same line.
Another proof: it is easy to see that as the vertex moves along the side of the base triangle, the third vertex moves in a straight line at a constant rate. Then the centroid moves also along a straight line. But it is easily checked what the centroids are at the beginning and end, and they are on the angle bisector. Thus all the intermediate centroids are also on the angle bisector.
Another solution: