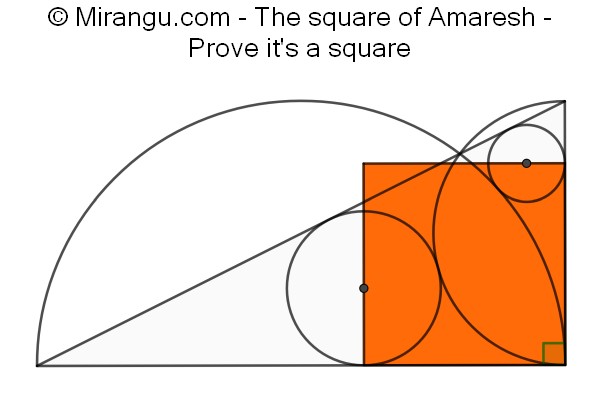
A right triangle having semicircles along its perpendicular sides and two smaller inscribed circles. Prove that the orange quadrilateral is a square.

Solution

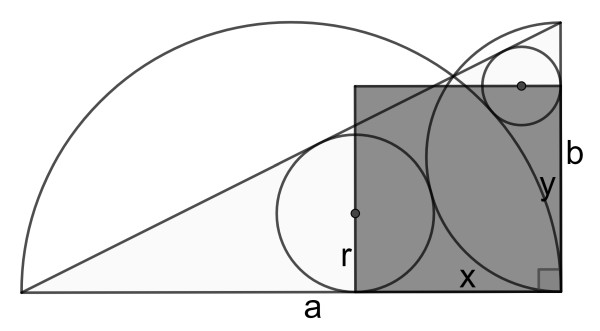
The perpendicular sides have length a and b. That the orange quadrilateral is a rectangle is straightforward from tangency to the small circles. Its sides have length x and y.

We use the solution of Peter Gallin to a previous puzzle. It says that r=(c-a)(c-b)/b, where c=√(a²+b²) is the length of the hypotenuse. Also it is well-known that the distance between the tangency points of two tangent circles to a common tangent is two times the square root of the product of their radii. Therefore x=√(2(c-a)(c-b)).

Now y can be calculated simply by exchanging a and b. But the expression for x is invariant under this operation, so y=x, making the rectangle a square.

This puzzle was inspired by Amaresh G S.