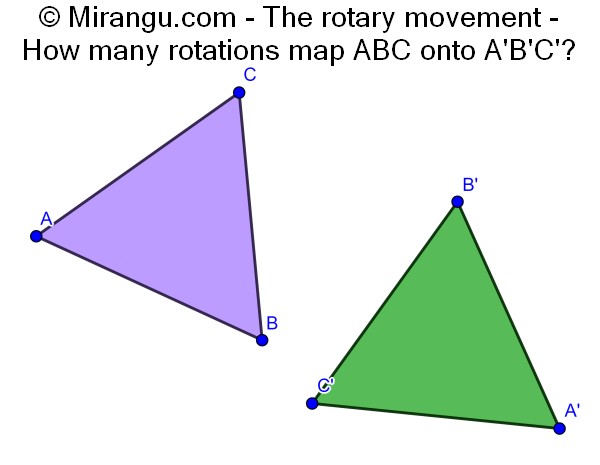
Two arbitrarily placed congruent equilateral triangles. Out of all the possible rotations of the plane, for how many will the image of ABC be A’B’C’?
Scroll down for a solution to this problem.
Solution
There is exactly one rotation, unless the corresponding sides are parallel, in which case there are none.
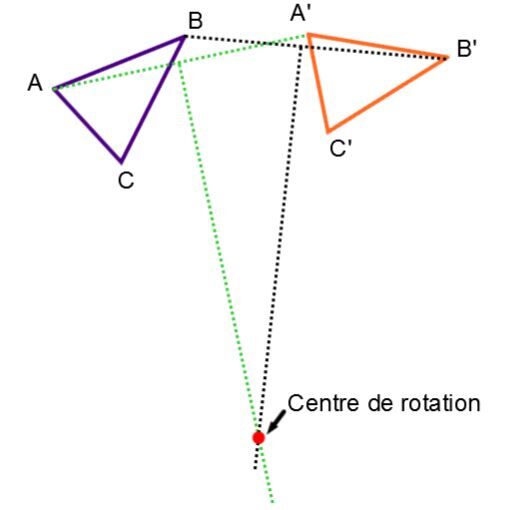
The first step is to find the location of the rotation centre by intersecting the perpendicular bisectors of AA’ and BB’. If AB and A’B’ are parallel, so will the bisectors be and they will not intersect. In this case there exists no rotation.
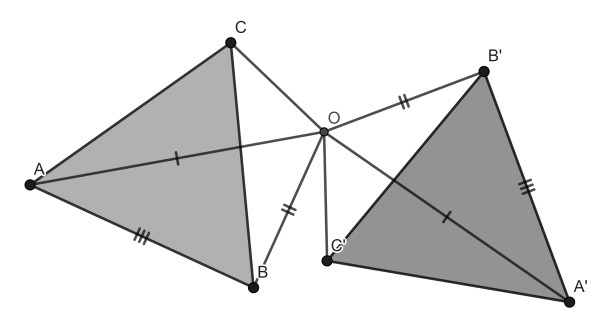
In all other cases there will be one possible rotation centre O. Now we have to prove that this O is also equidistant from C and C’. Looking at the figure above, we deduce from SSS that triangles ABO and A’B’O are congruent. Therefore angles OAC and OA’C’ are equal. From SAS it follows that triangles AOC and A’OC’ are congruent and hence OC and OC’ are congruent.
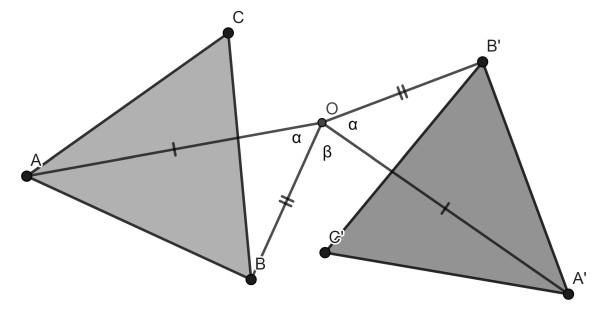
Finally, we must have that the rotation angles of the three vertices are equal. From the figure above we see that angle AOA’ equals α+β and so is angle BOB’. Therefore the are equal. Similarly they are equal to COC’.
Poem
Two twin triangles
Court hopefully each other
Every one does what must be done
And revolves around both
Successive rotations
So that everyone follows
His own desire
A reciprocal attraction
A very strong alchemy
Like the two poles of a magnet
Two poles of love
One reply on “The rotary movement”
1. If the corresponding sides are parallel, two rotations map ABC onto A’B’C’:
For example take an arbitrary point P and map ABC by point reflection at P (that’s a rotation with 180°) onto A”B”C”; then take the midpoint Q of A” and A’: point reflection at Q maps A”B”C” onto A’B’C’.
2. The argumentation for the general case is shorter, if we use the centres of the circumcircles of the triangles:
Let M resp. M’ be the center of ABC resp. A’B’C’, gM the perpendicular bisector of M and M’.
Then for any point R of gM the rotation with centre R and angle a(M, R, M’) maps M onto M’ and the circumcircle of ABC onto that oh A’B’C’.
If R is the point of intersection of gM and the perpendicular bisector of A and A’ then the rotation also maps A onto A’.
As rotation preserves angles, B is mapped onto B’ and C onto C’.