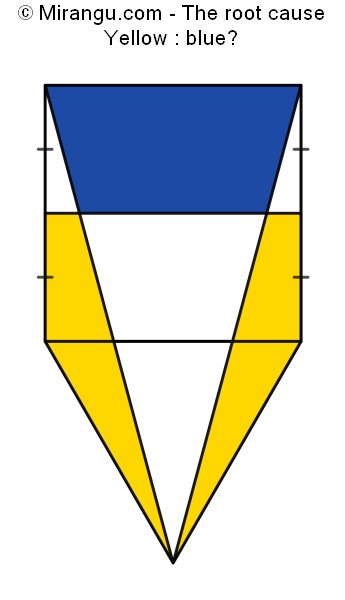
A square and an equilateral triangle are divided in several polygons. What is the proportion yellow : blue?
Scroll down for a solution to this problem.
Solution
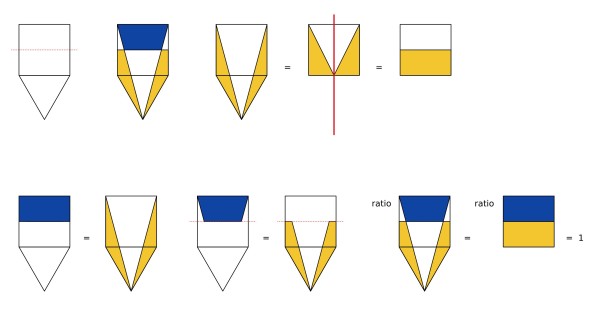
The proportion yellow : blue is 1 : 1.
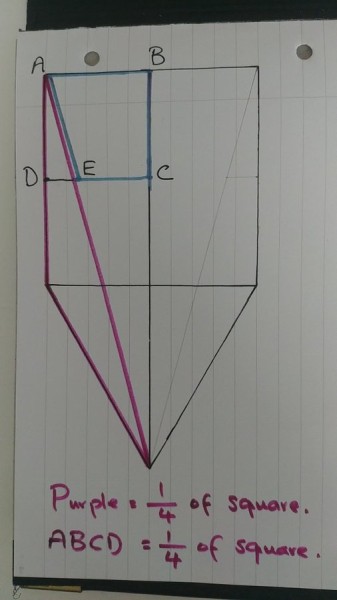
Thanks to @RonySarker71 I see the light, at last ☺
In my diagram, deduct area of ADE from that of “purple” and “ABCD” to prove that the remainders are also equal.
Visual solution
Poem
Why the root cause
For a painting remembering Mondrian ?
Specialist of abstract art
A special vocabulary
For figures of geometry
Such highly utopia
Mondrian says art is higher than reality
In order to create universal beauty
And intimate spirituality
To come close to harmony

One reply on “The root cause”
Let ABCD ( clockwise with A at top left) and DCE be the square and the equilateral triangle. F and G are the midpoints of AD and BC. AE and BE intersect FG at M and N respectively.
Let AB=2. By symmetry, the triangles ADE and BCE are congruent and also the triangles AFM and BGN.
Rectangle ABGF area is 2*1 = 2….
(1)
triangle ADE and BCE total area is 2*(1/2)*2*1 = 2…..(2)
Equating (1) and (2) and subtracting the sum of areas of the triangles AFM and BGN from both sides,
area of ABNM = sum area of FMED and GNEC.
which is same as,
Blue area = Yellow area.
Hence the ratio is 1:1.