Express the area of the orange triangle in terms of the areas of the other colours.
Scroll down for a solution to this problem.
Solution
Orange = (purple-blue-green)/2.
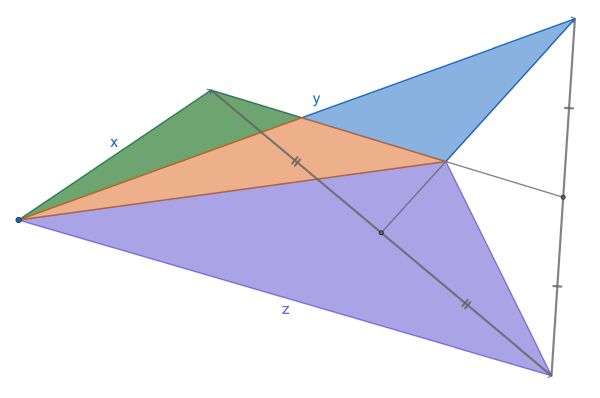
Let G denote the area of the green triangle, B the blue, P the purple, and O the orange. Add G to O, and B to O, getting triangles G’ and B’ sharing a common base with P. Let x, y, z be the vectors from the left endpoint of the common base to the tips (opposite the common base) of the G, B, and P triangles respectively.
Notice that the right endpoint of the common base is now the centroid of those three tips, so its vector is the average (x+y+z)/3 of the three. The area of G’ is (1/2) (x+y+z)/3 X x, where X denotes the cross-product for vectors.
Similarly, the area of B’ is (1/2) (x+y+z)/3 X y, and the area of P is – (1/2) (x+y+z)/3 X z. Then the sum of areas G’+B’ minus P is (1/2) (x+y+z)/3 X x + (1/2) (x+y+z)/3 X y + (1/2) (x+y+z)/3 X z = (1/6) (x+y+z) X (x+y+z) = 0, because the cross-product of a vector with itself is always zero.
But G’ = G + O, and B’ = B + O, so that gives G+O+B+O = P, or 2O = P – B – G, and finally O = (1/2)(P-B-G).
3 replies on “The paper airplane”
Here’s a proof without vectors – but didn’t come up with this until after reading the above proof that does use vectors.
Incomprehensible text.
When I constructed the puzzle, I thought it was an easy “quiz” for the understanding of the centroid of a triangle. When I read the puzzle now, and the solution, it seems complicated and tricky. It demonstrates that often it is easier to construct the puzzle than it is to solve the puzzle. And perhaps I “over-obfuscated” the idea. 🙂