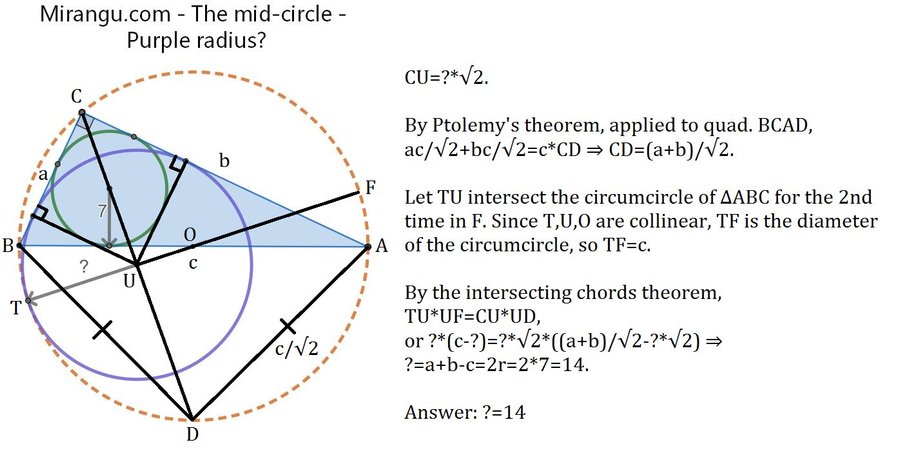
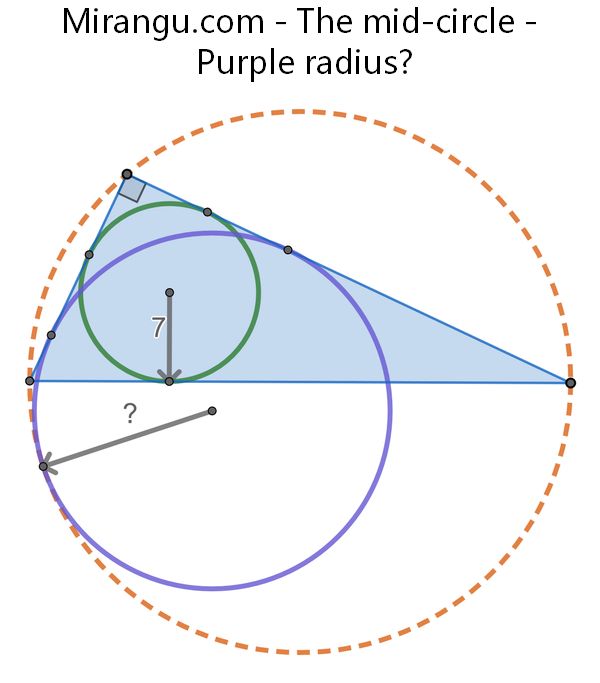
A blue right triangle has an orange-dotted circumcircle and a green incircle of radius 7. What is the radius of the purple circle, which is internally tangent to the orange circle and to the two sides of the right angle?
Scroll down for a solution to this problem.
The purple radius is 14.
A blue right triangle has an orange-dotted circumcircle and a green incircle of radius 7. What is the radius of the purple circle, which is internally tangent to the orange circle and to the two sides of the right angle? https://t.co/WkAhHhLDtY By @MarshallWBuck pic.twitter.com/6qCZOx7oDo
— Mirangu (@Mirangu1) January 9, 2024
One reply on “The mid-circle”
14. If the right triangle has sides a, b, c, then the incircle has radius (a+b-c)/2, and the purple mixtacircle has radius a+b-c. Thus, the purple circle has twice the radius of the green circle.
Proof of the mixtacircle radius formula in this case:
The center of the circumcircle is the midpoint of the hypothenuse c. If the radius of the mixtacircle is r, then the coordinates of the center of mixtacircle, relative to the right angle corner, is (r,r), and distance from the circumcenter (a/2,b/2) is the square root of (r-a/2)^2+(r-b/2)^2, but should also be (r-c/2). This gives the equation r^2 = (a+b-c)r, from which we get r = a+b-c.