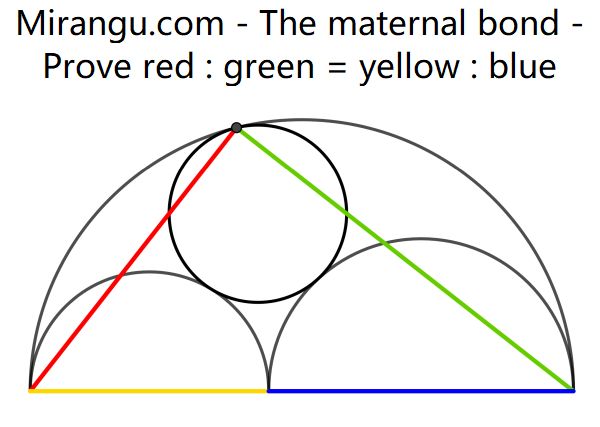
Three tangent semicircles and a circle. One tangency point is shown. Prove that red : green = yellow : blue.
Scroll down for a solution to this problem.
Solution
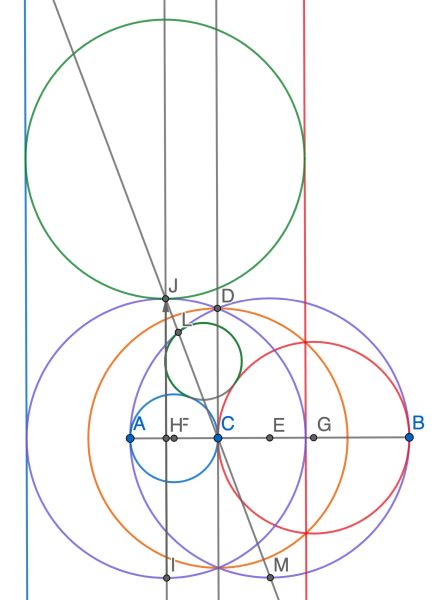
In the diagram, I extend the semicircles into the red, blue, and purple circles. I notice that we want to show that the line LC bisects the right angle ALB at L, and that means that we want to show that the line LC goes through the bottom point M of the right-hand purple circle. I then invert with respect to the orange circle with center C and radius CD. The purple circle’s image has the same radius and has shifted to the left, but the red circle and blue circle turn into vertical lines, and the green circle’s image fits between those lines, and touches the left-hand purple circle at its top point J. But J and L are both on a line through the center of inversion C, and the purple circles are reflections about the line DC, and 180 rotations around the point C, so the line JL goes through the bottom point M of the right-hand purple circle. QED
Poem
The maternal bond
Is an indestructible bond
Being mother is an unique experience
It starts with the umbilical cord
Being a mother
No one can understand it
If they haven’t lived it
It’s almost
A love addiction