A cyclic quadrilateral with its diagonals and two altitudes. Prove that AB is parallel to EF.
Scroll down for a solution to this problem.
Solution
Categories
The inner parallel
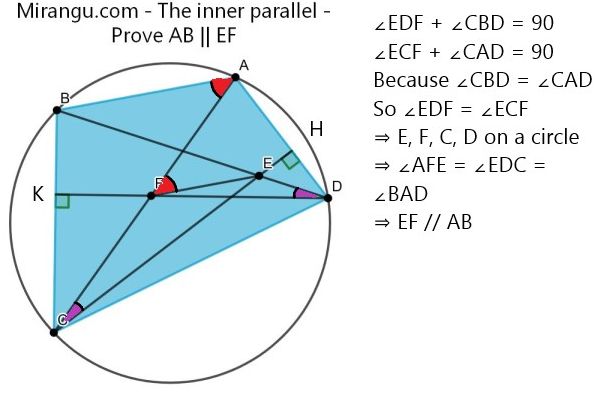
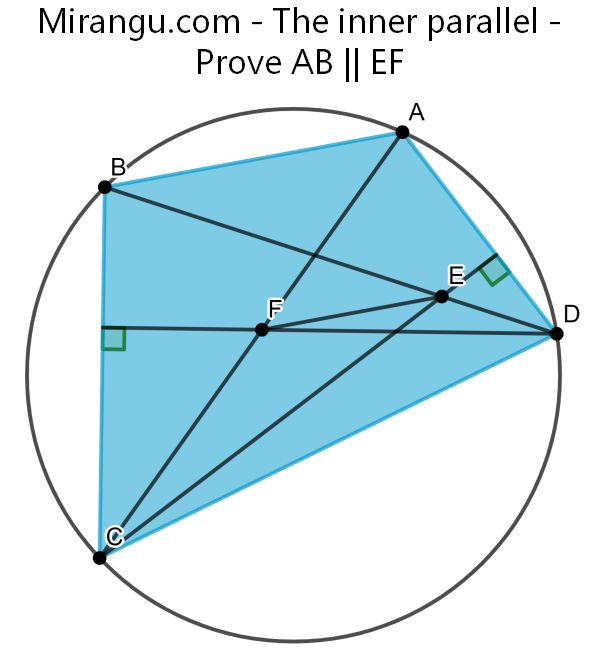
A cyclic quadrilateral with its diagonals and two altitudes. Prove that AB is parallel to EF.
Scroll down for a solution to this problem.
A cyclic quadrilateral with its diagonals and two altitudes. Prove that AB is parallel to EF. https://t.co/rLWkeOw6rr pic.twitter.com/xZv4OQbCSl
— Mirangu (@Mirangu1) November 30, 2022
5 replies on “The inner parallel”
The following Lemma (in the diagram) can be used for a proof of this problem.
The line connecting the bases of the altitudes is parallel to the top edge of the quadrilateral, so the Lemma applies.
I do not yet have a proof of the Lemma, but it appears to be a result in Projective Geometry and generalizes as shown in this diagram.
With projective geometry, it suffices to prove the Lemma in the case of 3 parallel lines intersecting 3 other parallels, perpendicular to the first set. Then, the result can be shown using simple coordinate algebra.
This is just the projective dual of the famous Pappus’s Theorem, so nothing new at all. Oh, well…
It looked familiar! Indeed, Pappus strikes again.