A square, a circle and its centre. Prove that the six red points are on one circle.
Scroll down for a solution to this problem.
Solution
Poem
In Ukraina something is happening
I see an unavoidable pattern emerging
This unacceptable behaviour is troubling
A lot of questions arising
A real disaster is in the making
War is killing and destroying
We are so far away and so near
We all are stunned and have fear.

One reply on “The emerging pattern”
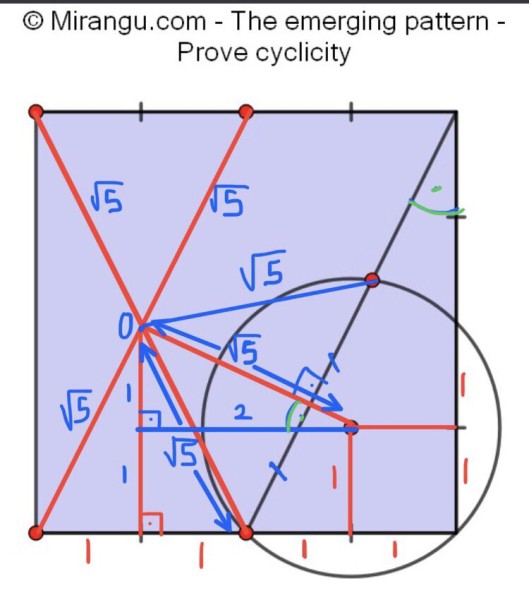
Let the six points be A to F clockwise starting from top left corner.
Let AE and BF intersect each other and O. AE, BF being diagonals of a rectangle, O becomes center of the required circle. Join OC, OD, CE, CD, DE. The two triangles OCD and ODE can be shown congruent using chord and radius properties. This gives OC=OE.
Let AC and ED meet at M on the right vertical side of the outer square.
angle CME + angle CEM = 90 degree.
angle ODE + angle CEM = 90 degree.
Hence angles CME and ODE are equal.
Also angles OEM and CME are equal being the angles of isosceles triangle AEM.
Hence angles ODE and OEM are equal. Thus the triangle ODE is isosceles, giving OD=OE.
Thus all six lines OA, OB, OC, OD, OE, OF are equal and form the radii of a circle.