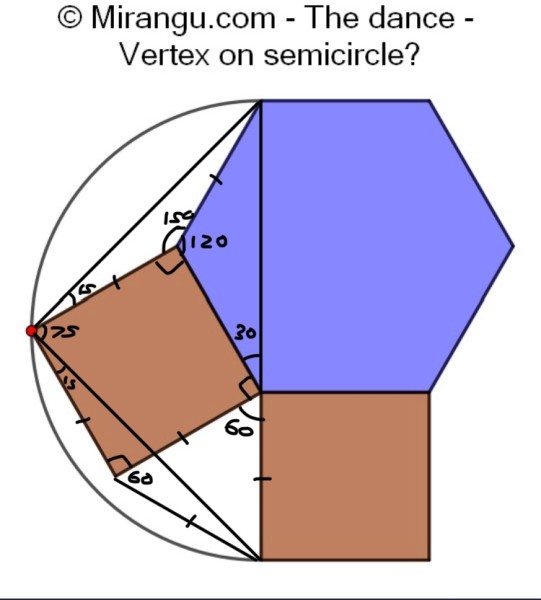
A regular hexagon, two squares and a semicircle connecting two vertices. Is the red vertex located on the semicircle?
Scroll down for a solution to this problem.
Solution
Yes, the vertex is on the semicircle, because the angle in the semicircle is 15°+75°=90°.
Poem
The dance
Dancing day and night
Having fun and glide
With a dancer, my inspiration
He is my guide and vision
We perform every hour
With some friends on the floor
Moving with our drums
Dancing in our own rhythm
Stepping and twirling
Letting the fire burn
To inspire our souls

One reply on “The dance”
Let the hexagon be ABCDEF clockwise with AB top horizontal side and the two squares be EDGH and FEIJ.
Let the side of hexagon be 2. Join AJ, JH and JE
In triangle AJE, AE=2√3, JE = √8 and angle AEJ = 45+30=75. Using cosine rule, AJ^2= 14.9282.
In triangle JEH, EH=2, JE = √8 and angle JEH = 60+45=105. Using cosine rule, JH^2 = 14.9282.
Also AH^2 = (AE + EH)^2 = (2*√3 + 2)^2 = 29.8564.
From triangle AJH, using above three values, the triangle is found to be a right angled triangle with angle AJH = 90°
Hence the point J must be on the circumference of the semicircle shown.