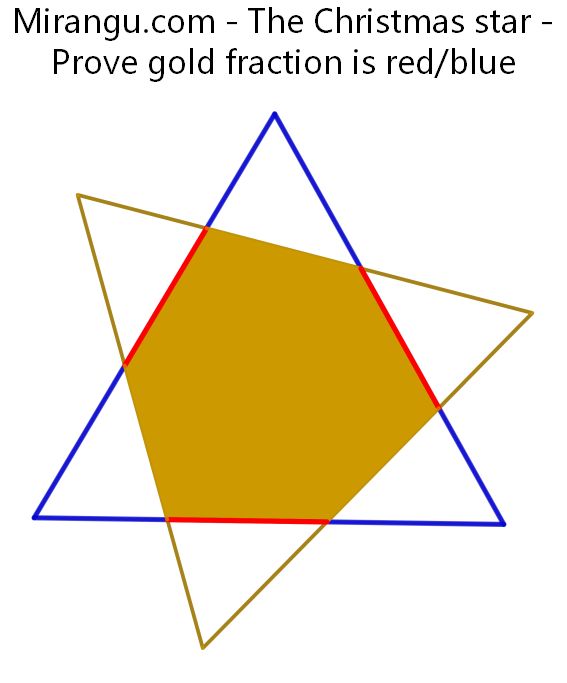
Two congruent concentric equilateral triangles. Prove that the gold fraction is red/blue.
Scroll down for a solution to this problem.
Solution
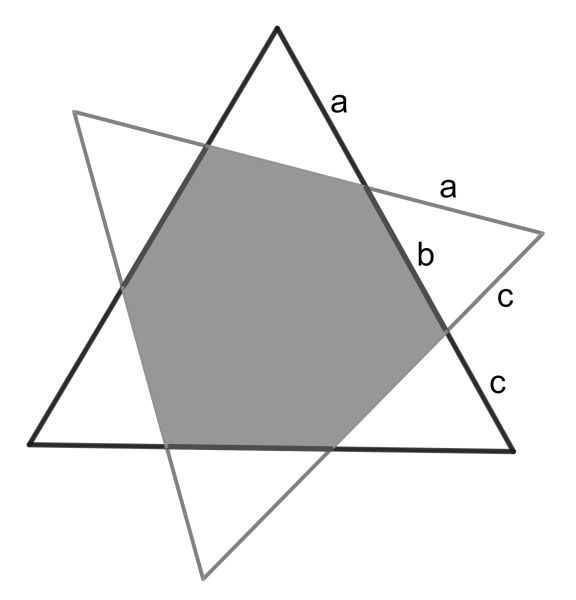
Because the triangles are congruent and concentric, symmetry implies that all six non-overlap triangles are congruent. They have sides a, b and c and an angle of 60° between sides a and c. Their area is √3ac/4.
It is easy to show that the total area is that of one equilateral plus three of those smaller triangles, whereas the gold overlap region is one equilateral minus three of these triangles.
So, total area T=√3(x2+3ac)/4 where x=a+b+c is the side length of the equilateral triangles. The overlap region O=√3(x2-3ac)/4. Working out the fraction, we get O/T=b/(a+c). But red is 3b and blue is 3(a+c). This completes the proof.
Poem
The christmas star
A hope from above
It’s like a sun
Shining and guiding us
The bride of the moon
She is the messager
Of a more fraternal and freer world
In peace
No more war
It is a symbol of sharing
And of solidarity actions
Tonight it lights up
The proud Xmas tree