Three parallelograms are inscribed in a circle. Prove that the common red vertex is the orthocentre of the dashed triangle.
Scroll down for a solution to this problem.
Solution
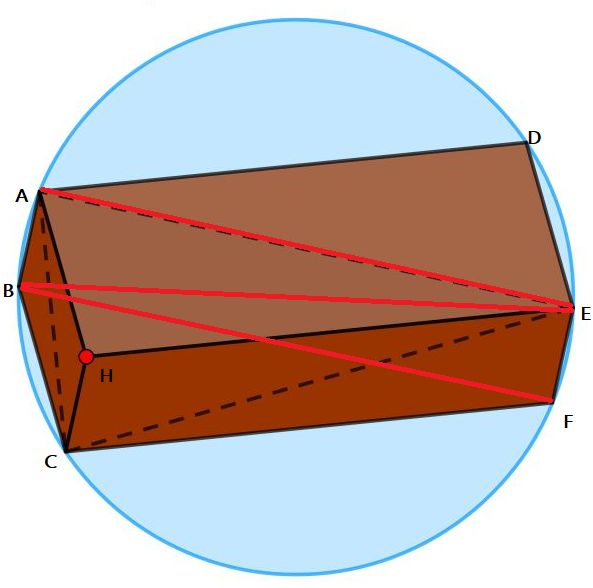
AB and EF parallel and same length implies BE diameter. Implies angle BAE 90. Implies CH, which is parallel to AB, is perpendicular to AE. Similarly AH is perpendicular to CE etc.
One reply on “The beam in your eye”
If you shrink the circle to half size towards the orthocenter H you obtain the famous “9 point circle of the dotted triangle AEC. The 9 points are: the midpoints of the sides, the base points of the altitudes and the midpoints between the vertices and H.