A quadrilateral and an internal point from which four line segments are drawn, each parallel to a different side. What is blue : orange?
Categories
A limited scope
Tag: quadrilateral
Categories
Cyclic quad festival
A triangle ABC with points D on AB, E on AC, and F on BC, such that ACFD and AEFB are cyclic quadrilaterals. Let DC and BE intersect at I. Show that AEID, CFIE, and BDIF are also cyclic quadrilaterals.
Categories
Ace of diamonds II
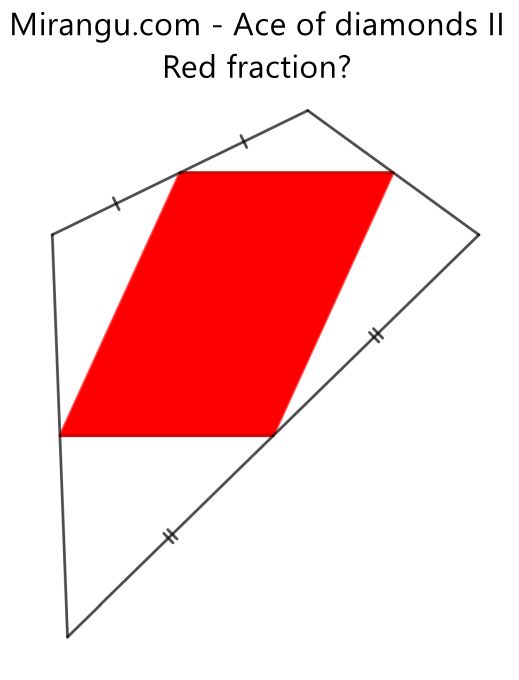
A parallelogram is inscribed in a quadrilateral. What fraction is red?
Categories
On all fours
Four coupled squares. Prove that the green and red quadrilateral have equal areas.
Categories
The cheese slicer
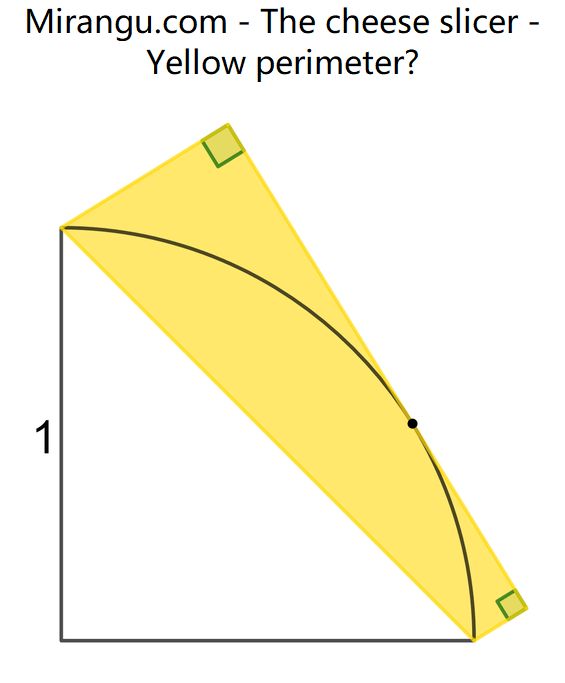
A quarter circle of radius 1 with a yellow quadrilateral that has one side tangent to it. What is the perimeter of the quadrilateral?
Categories
Tip of tipi
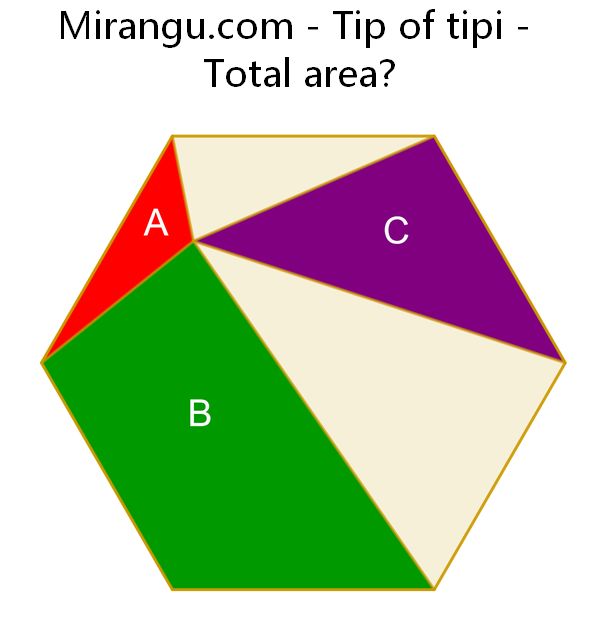
A regular hexagon is divided in four triangles and one quadrilateral. Express the hexagon area in terms of areas A, B and C.
Categories
Bicyclic transport
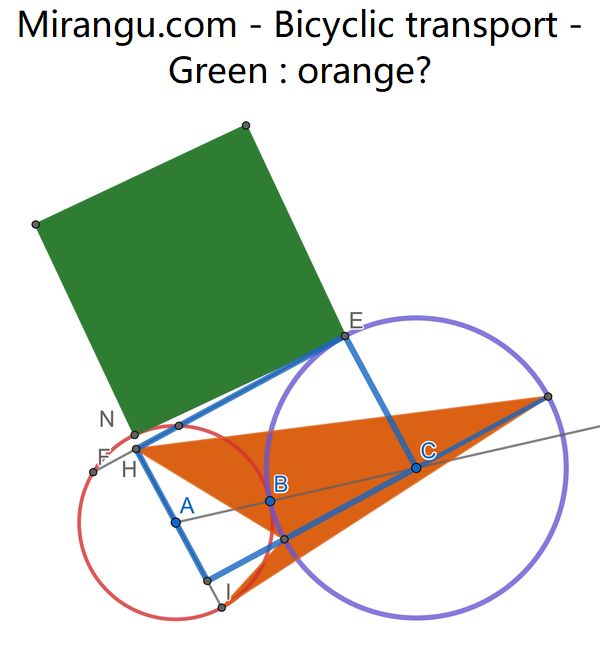
EHF is tangent to the purple circle at E, and EN is tangent to the red circle at N. A and C are the circle centers. A blue rectangle has three corners HEC and the point A on one side. What is the ratio of areas, green square to orange quadrilateral?
Categories
Quad stretches
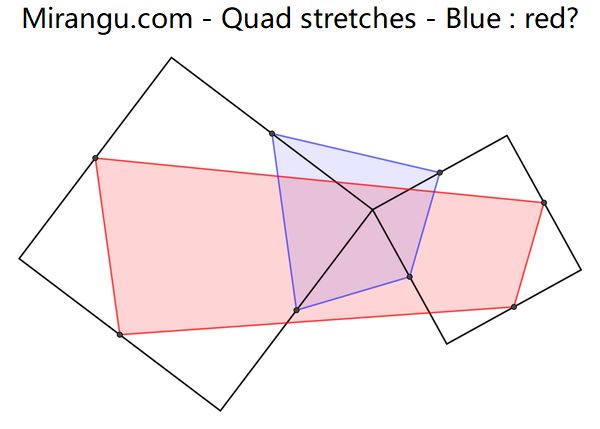
Two squares sharing a vertex and two overlapping coloured quadrilaterals from square side midpoints. What is the area proportion of the blue and the red quadrilateral?
Categories
Touch the sides
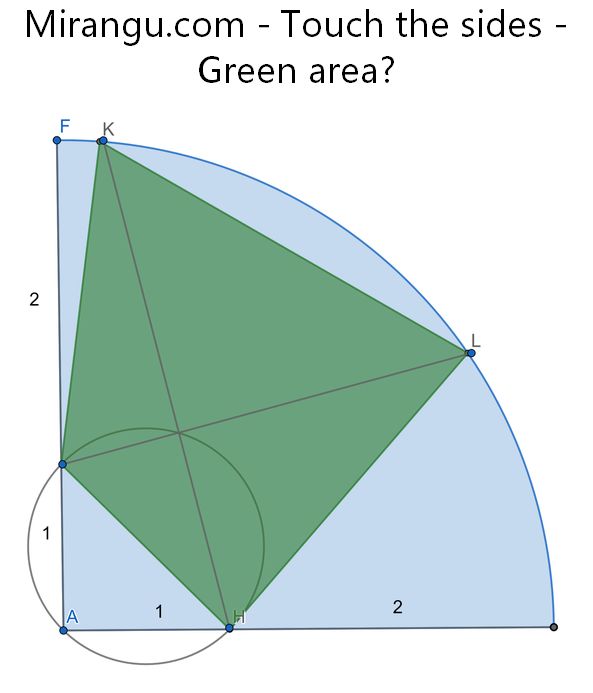
What is the area of a green quadrilateral that fits inside a quarter circle, and has perpendicular diagonals?
Categories
Squaring the quad
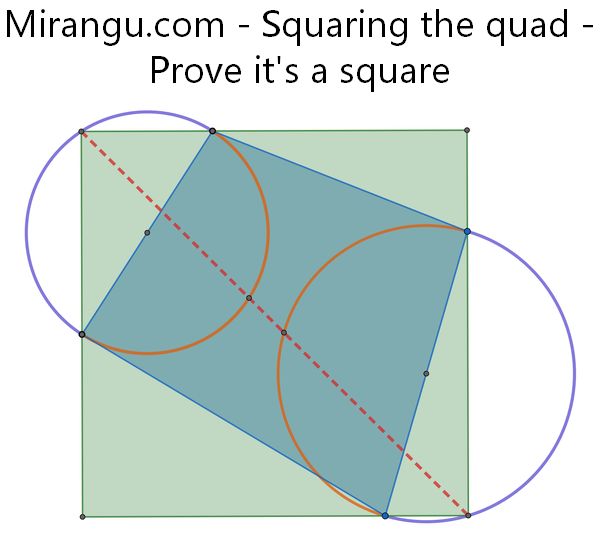
Form inward semicircles (orange) and outward semicircles (purple) on two opposite sides of a quadrilateral. Connect the midpoints of the orange arcs, intersecting with the purple arcs. Show that you obtain two corners of an enclosing square.