Four squares are placed as shown. Prove that the green quadrilateral is a parallelogram.
Stretch of imagination
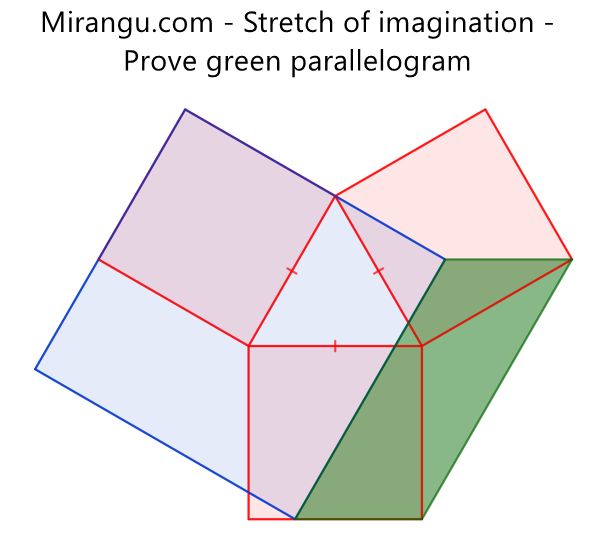

Four squares are placed as shown. Prove that the green quadrilateral is a parallelogram.
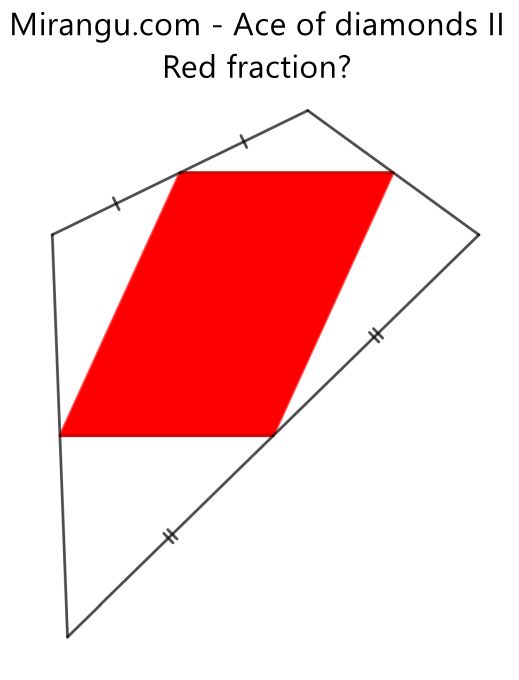
A parallelogram is inscribed in a quadrilateral. What fraction is red?
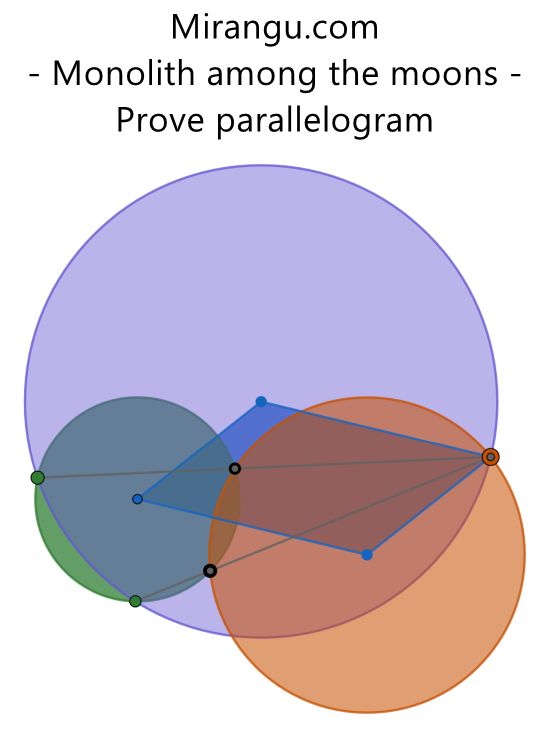
The points of intersection of the purple and green circles line up with the points of intersection of the green and orange, lines meeting on the orange circle. Show that the circle centers plus the orange point form a parallelogram.
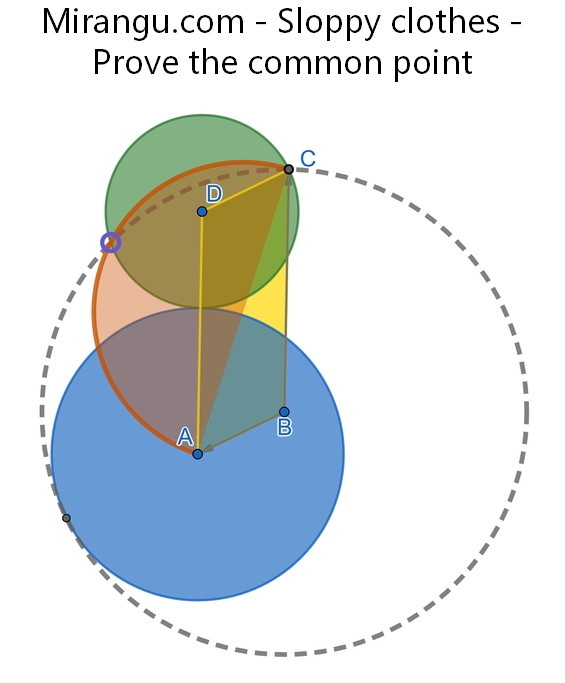
Green and blue tangent circles, with centers A, D. Parallelogram ADCB, with C on the edge of the green. Red semicircle on diameter AC. Dotted circle through C with center B. Show that the green, red, and dotted arcs have a common point.
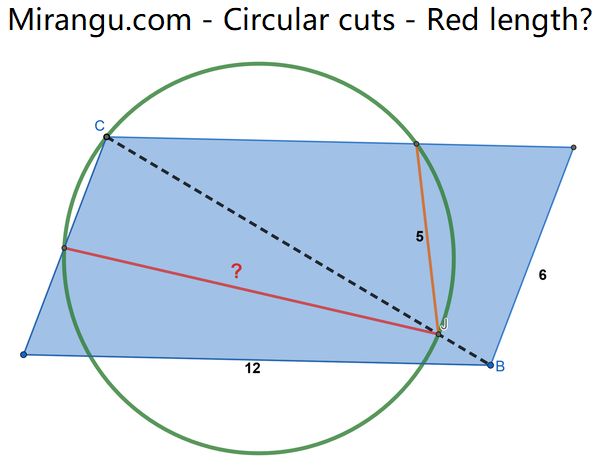
The blue parallelogram’s vertex C lies on a green circle that intersects the diagonal BC at J. What is the length of the red segment?
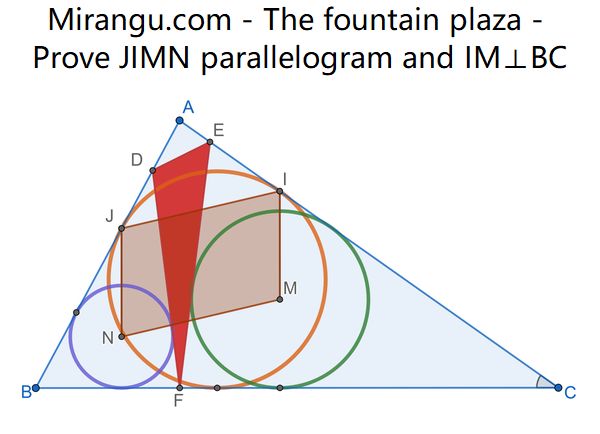
The incircle of ABC touches sides at I and J. D, E, F are the bases of altitudes from C, B, and A. The incenters of BDF of CEF are N and M, respectively. Show that JIMN is a parallelogram and that IM is perpendicular to BC.
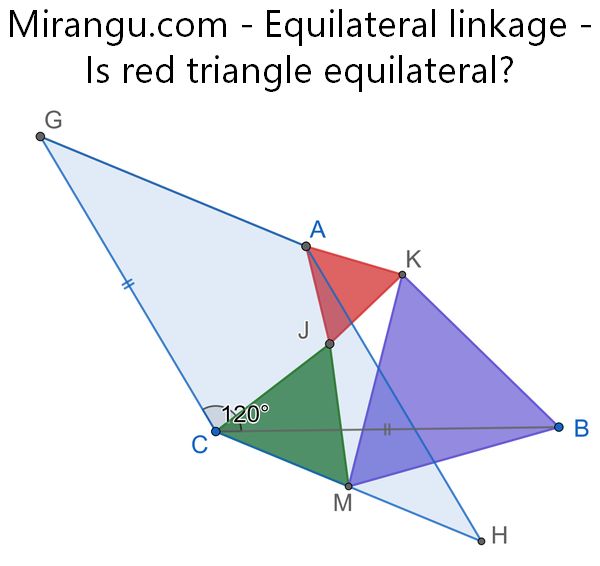
Given 3 points A, B, C, define G so CG=CB and angle GCB is 120 degrees. Define M as the midpoint of side CH of the parallelogram CGAH. The green equilateral has side CM and the purple equilateral has side MB. Is AJK also equilateral?
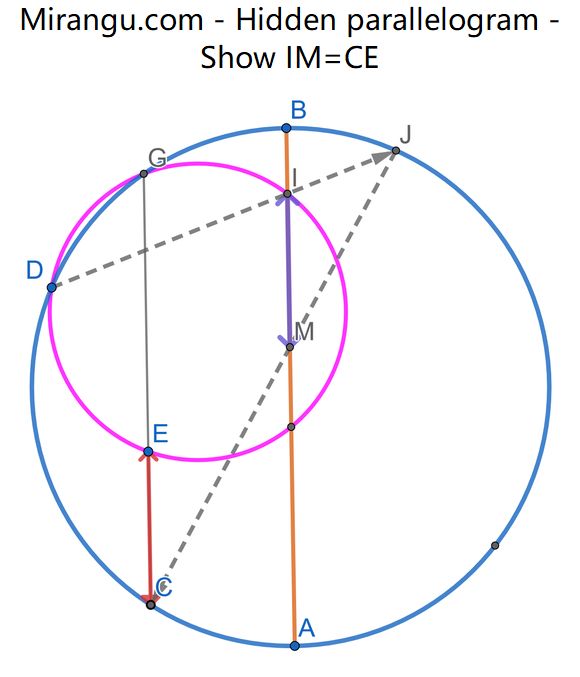
Blue circle (ACDGB) with CEG || AB. Pink circle (EDG) intersects AB at I. Extend DI to intersect blue circle at J, then JC intersects AB at M. Show that IM = CE.
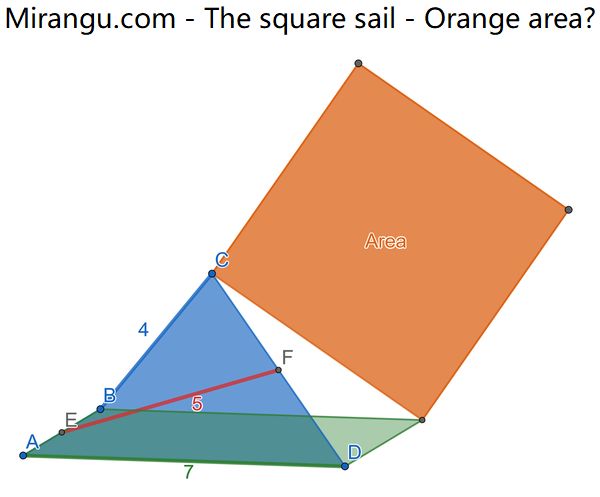
A quadrilateral and a parallelogram share two sides, and a vertex from each determine the orange square. The lengths BC, EF, AD are 4,5,7 respectively, where E and F are midpoints of AB and DC. What is the orange area?
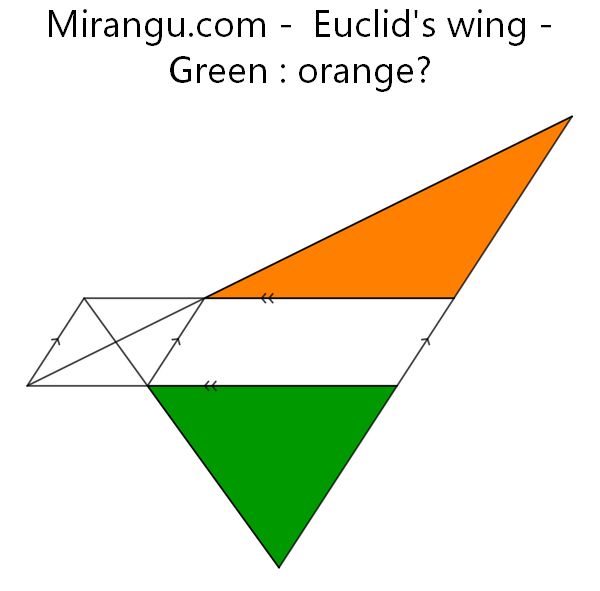
Several line segments, some of which are parallel. What is green : orange?
Improve your mental health with our new book “Vitamin G, 100 wholesome geometry puzzles”.
Order now