Two squares share a vertex. The shown vertex can lie anywhere on the lower side. What is the maximum of red/blue?
Categories
Slip sliding
Tag: maximum
Categories
Dog ear III
A square and a 45° angle. The blue point can slide along the top side. If the red fraction is maximal, what is blue : yellow?
Categories
Maximum range death ray
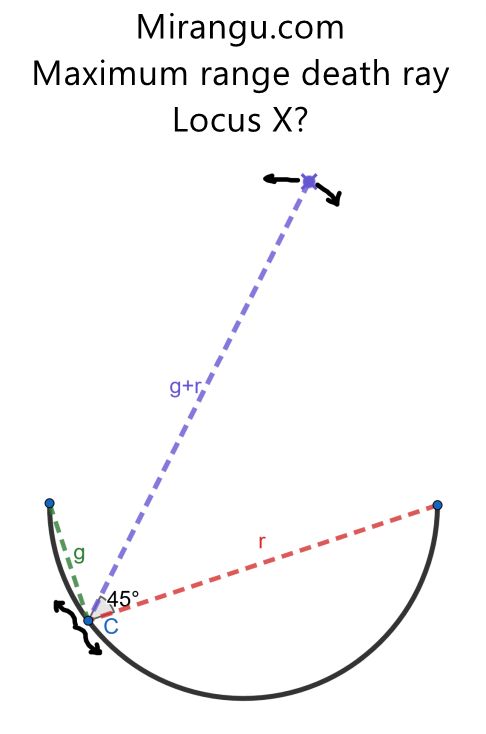
The death dish is semicircular, with point C for aiming the ray, which bisects the green and red lines. The maximum range of the death ray is the sum of the red and green lengths. What is the locus of the maximum point X as C varies?
Categories
Filling the bowl
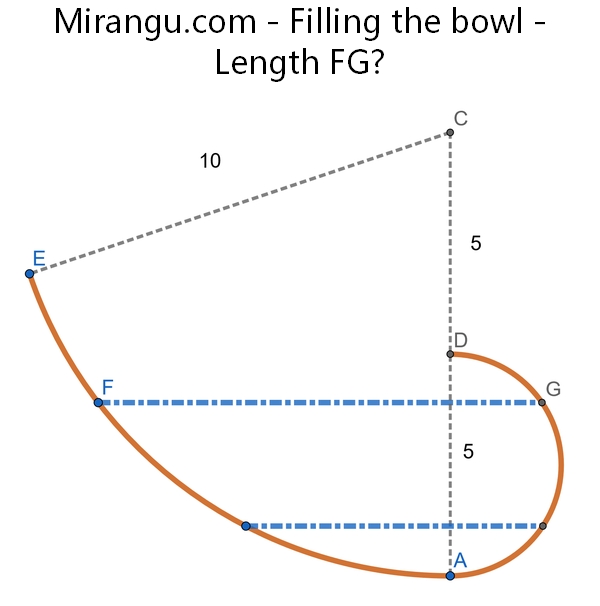
We add water to the bowl until the surface line FG has maximum length. What is the length FG? (DGA is a semicircle, and AFE is a circular arc with center C.)
Categories
Falling in
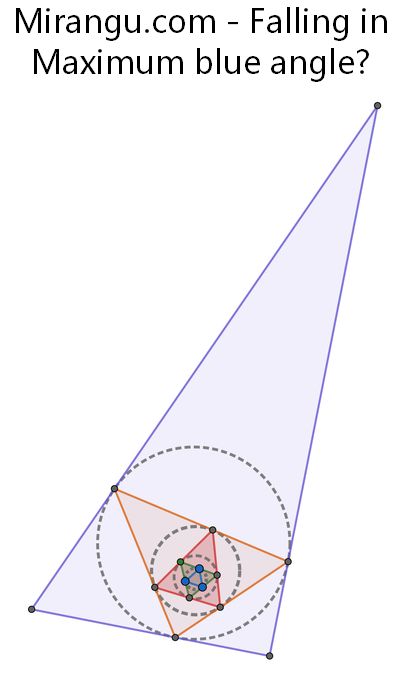
Start with an acute triangle and form a new triangle from the points of tangency of its inscribed circle. Continue this process to make make the triangle with blue vertices. What is the maximum possible angle at a blue vertex?
Categories
The grassy knoll
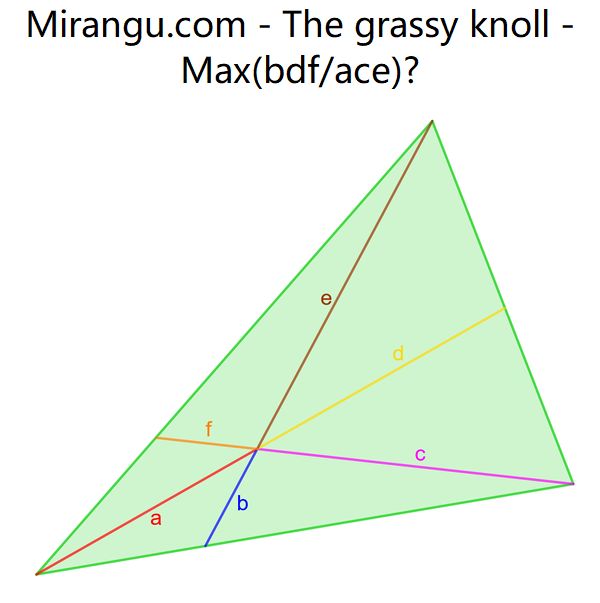
A triangle with three cevians that are concurrent in an arbitrary interior point. What is the maximum value of bdf/ace?
Categories
To the max
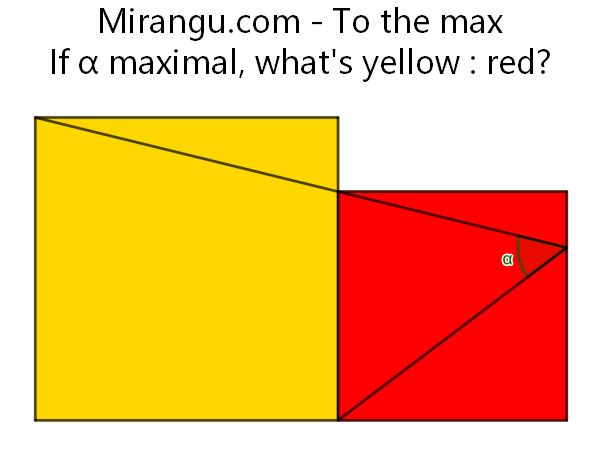
Two squares and two line segments. If the angle α is maximal, what is yellow : red?
Categories
The oppressed minority
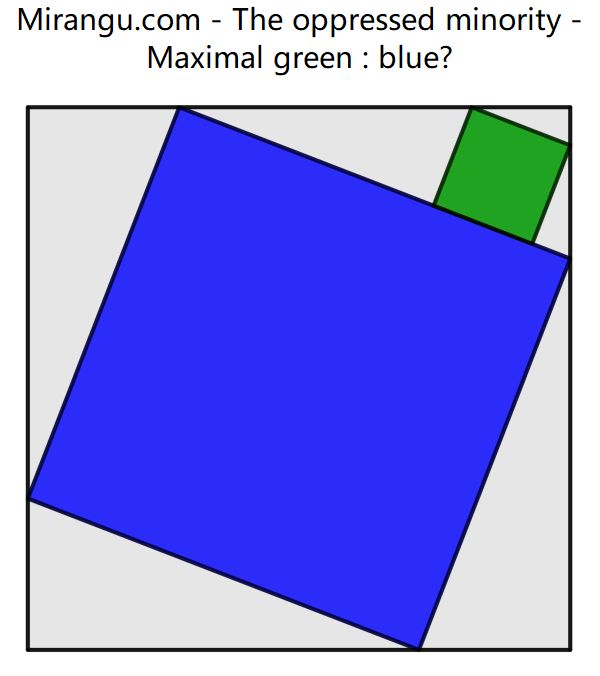
A square with two inscribed squares. What is the maximal proportion green : blue?
Categories
La Sagrada Familia
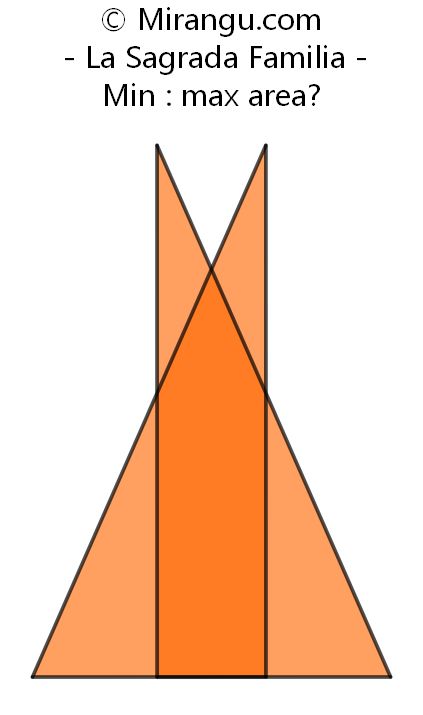
Two congruent right triangles on a common baseline have an overlap of variable size. What is the proportion of the minimal area to the maximal area?
Categories
The maxbox
A square containing a red square of variable size sharing a vertex with a blue rectangle. What is the maximal blue fraction?