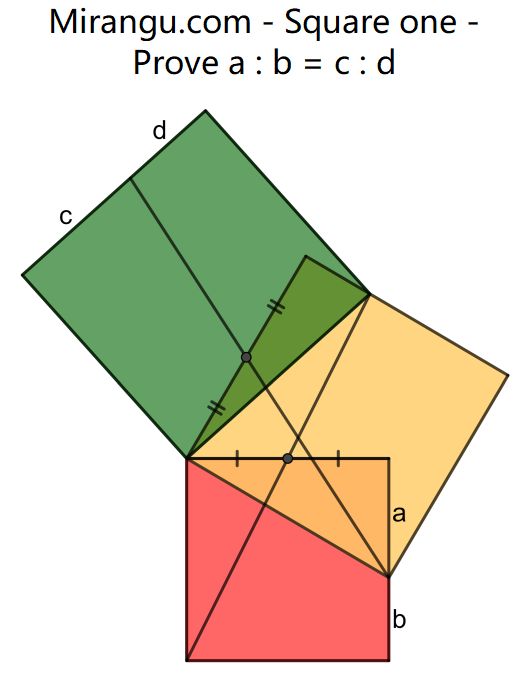
Three squares share a vertex. Two line segments pass through side midpoints. Prove that a : b = c : d.
Scroll down for a solution to this problem.
Solution
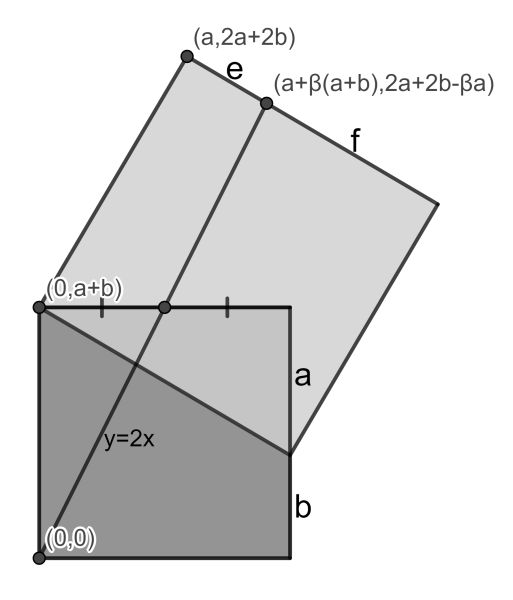
This problem can best be seen as twice an easier one. The red and orange square are arranged in the same way as the orange and the green one, namely as shown in the figure.
Let’s consider this configuration then. Using Cartesian coordinates and triangle congruence, the coordinates of the selected points can easily be found. Note that β=e/(e+f). Since the farthest point is on the line y=2x, we have 2a+2b-βa=2[a+β(a+b)]. This can be rewritten as 2-αβ=2α+2β, where α=a/(a+b).
Crucially, this equation is symmetric under the exchange of α and β. So, if β=F(α), we equally have α=F(β). In other words: the function F is equal to its inverse. Returning to our original problem, going from a : b to e : f to c : d one has to apply F twice, but this is equivalent to the identity function. Therefore a : b = c : d.