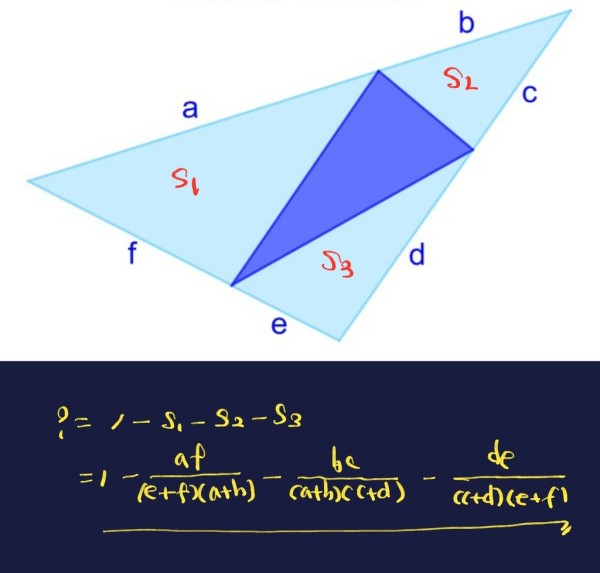
A triangle with an inscribed triangle. What fraction of the former does the latter cover in terms of lengths a, b, c, d, e and f?
Scroll down for a solution to this problem.
Solution
The shaded fraction is (ace+bdf)/((a+b)(c+d)(e+f)).
Poem
Spiegel im Spiegel
Mirror in the mirror
In Tallin
Arvo Pärts composition
This piece is made for meditation
For a form of contemplation
Piano and violin
Play with tintinnabull
Bells which sound in this melody
Showing new mirrors for tranquillity
Pictures to swallow immediately

2 replies on “Spiegel im Spiegel”
The 1962 Putnam exam problem:
A3. ABC is a triangle and k > 0. Take A’ on BC, B’ on CA, C’ on AB so that AB’ = k B’C, CA’ = k A’B, BC’ = k C’A. Let the three points of intersection of AA’, BB’, CC’ be P, Q, R. Show that the (area PQR) (k^2 + k + 1) = (area ABC) (k – 1)^2.
I remember Harvey Cohn coming into the room for a few minutes, working the 3 hour exam in a few minutes, then leaving the answers in the trash on the way out. After the exam, we looked at his solution to problem A3, and he used the results on the determinant of the 3 by 3 matrix formed from the barycentric coordinates of the inside triangle. The matrix has first row (1,k,k^2) divided by 1+k+k^2. the other rows are cyclic shifts.
(I was 15 at the time, and was very impressed!)
sorry – here comes the corrected version.
Please delete the first picture