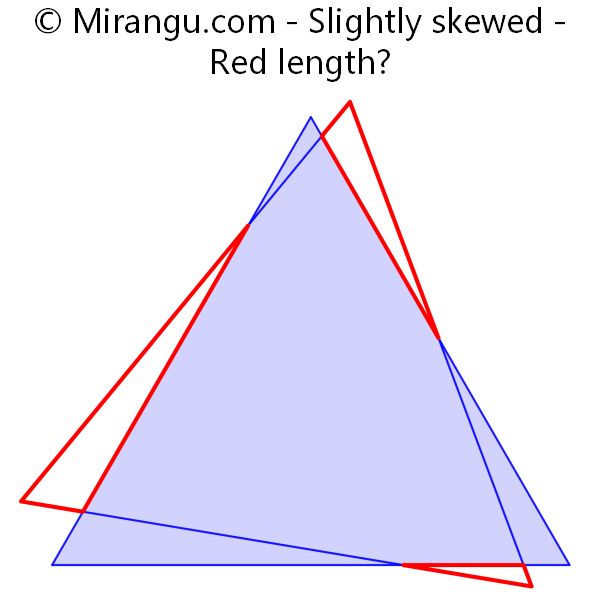
Two overlapping equilateral triangles with side lengths 1. What is the total red length?
Scroll down for a solution to this problem.
Solution
The red length is 3.
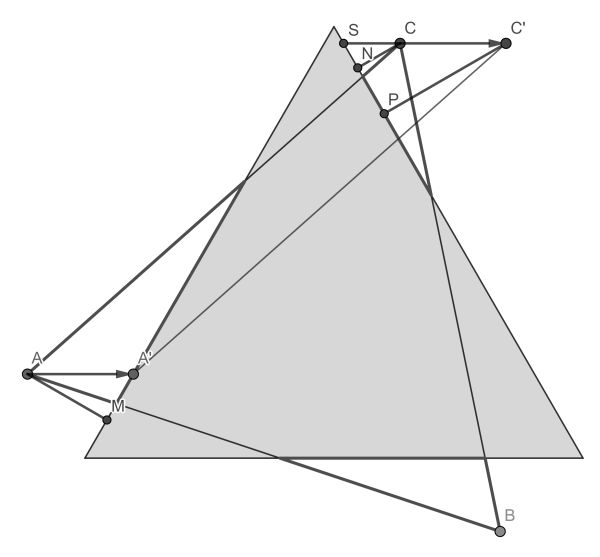
The first part of the solution is proving that there is translational invariance. Suppose we translate the skewed equilateral triangle along the horizontal side of the other. Clearly, the bottom red triangle does not change. But the sum of the other two perimeters does neither.
The total perimeter of those similar triangles is proportional to the sum of their heights. Looking at the diagram above, this sum is |AM|+|CN|. Translating from A tot A’and C tot C’, the sum of their heights becomes |PC’|. But from the 30-60-90 triangles that is equal to |AM|+|CN|. And that goes for any translation along the horizontal. The total perimeter is therefore invariant under translations along the straight equilateral triangle sides and hence under all translations.
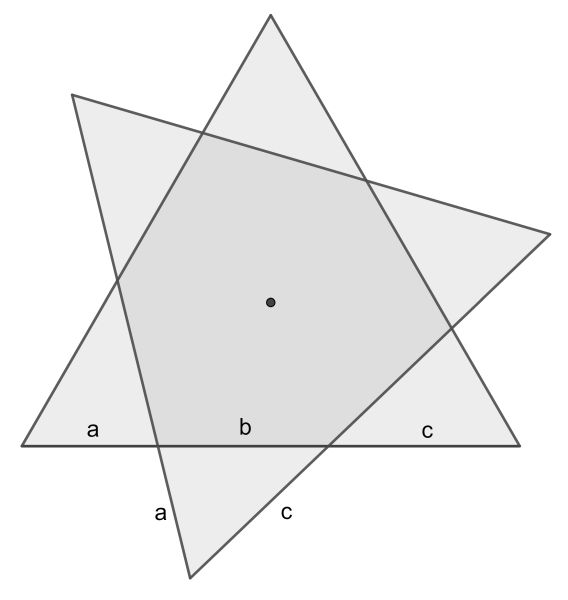
Now we are allowed to translate such that the two equilateral triangles are concentric. It is easy to see that all six non-overlap triangles are congruent and have perimeter a+b+c. But this equals the side length 1. So the total red perimeter is 3.
Poem
The triangle encloses the diamond
The angles are out
A wonderful escape