If you roll a circle down a parabola, small circles can roll all the way down and up, whereas large circles get stuck between the sides at some point. What is the transition radius? In other words, what’s the maximum circle that keeps on rolling?
Scroll down for a solution to this problem.
Solution
The maximum rolling circle has radius 1/2.
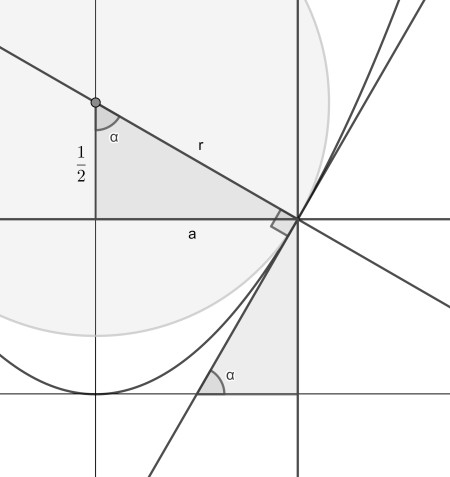
We will calculate the x-coordinate of the touch point of a larger circle. Call it a (the other touch point will have -a). Now we can draw the two triangles from the touch point using the radius and the tangent as shown.
The angle α has a tangent of 2a, being the derivative of x2 at x=a. From rotational symmetry, the angle at the circle centre is also α. Therefore we know that the side along the y-axis has length 1/2.
Applying the Pythagorean theorem we know that a2=r2-1/4. So, at r=1/2 the two touch points coincide. This is the maximum rolling radius.
Poem
The Rolling Stone
That is the Sisyphus story
Pushing up to the mountain
A great stone from the earth shining beauty
Rolling it ceaselessly
From the bottom to the top
For humankind absurdity
This myth is an allegory
For our day to day activity
Please don’t forget to be happy
One reply on “The rolling stones”
A second way:
We start with a circle k touching the parabola in the origin:
k: x² + (y – r)² = r²
p: y = x²
To calculate the points of intersection
of k and p we solve the equation
x² + (x² – r²) = r²
and we get
x²·(x² – (2·r – 1)) = 0
The solutions are:
x_1/2 = 0 and (if r ≥ ½) x_3/4 = ± √(2·r – 1)
We get the maximum circle that rolls down to the origin with r = ½.
If r is greater than ½ the circle will get stuck between the
points P_3 and P_4 with P_3/4(± √(2·r – 1)| 2·r – 1).