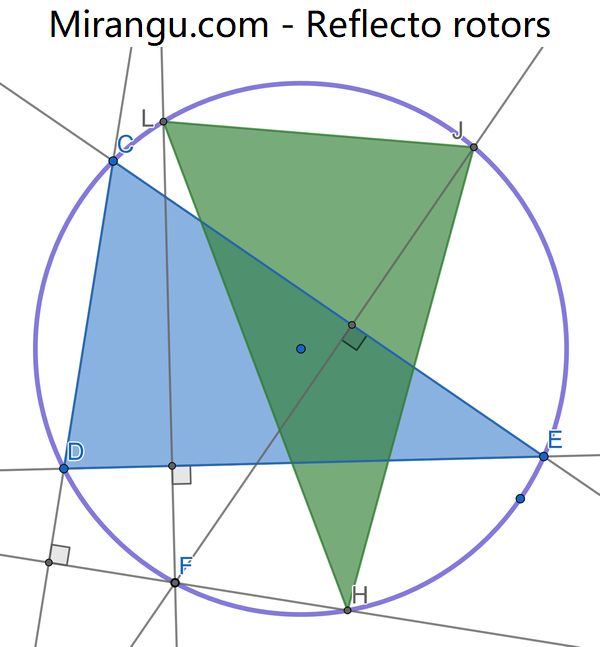
Fixed rotor (triangle) CDE inscribed in purple circle. Moving point F on the circle. Define for the point F a new rotor HJL on the circle, such that FH, FJ, FL are perpendicular to CD, CE, and DE respectively. Show that the green triangles HJL do not change shape as F moves.

Solution

In F : a is equal to <H and <E => a constant. c is equal to <D => c constant => b is constant ( = 180-a-c) but b is equal to <L so all angles constant in LJH. moreover, LJH is similar to CDE.

Fixed triangle CDE inscribed in circle. Define for point F a new triangle HJL on the circle, such that FH, FJ, FL are perpendicular to CD, CE, and DE respectively. Show that the triangles HJL do not change shape as F moves on the circle. https://t.co/MuRIBCmut6 By @MarshallWBuck pic.twitter.com/v2tJRliI8Y

— Mirangu (@Mirangu1) June 6, 2024