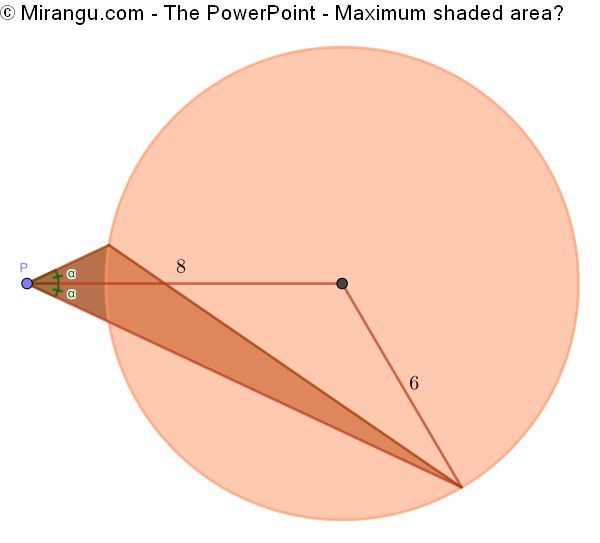
A point lies 8 from the centre of a circle of radius 6. The angle α is variable. What’s the maximum triangle area?
Scroll down for a solution to this problem.
Solution
The maximum area is 14.
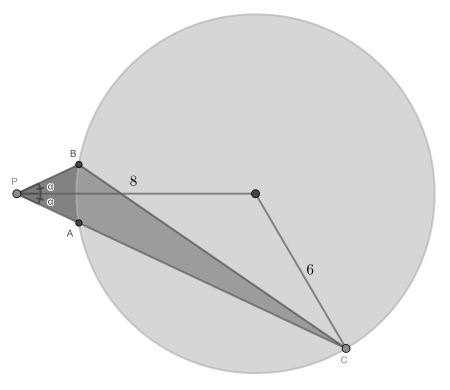
The area of the triangle is |PB|*|PC|*sin(2α)/2. Now because of reflection symmetry in the line through P and the circle centre, we see that |PB|=|PA|.
Next, we use the Power-of-a-point theorem, which says that |PA|*|PC|=82-62=28. So A(α)=14sin(2α). Clearly, this has a maximum of 14 at α=45°.