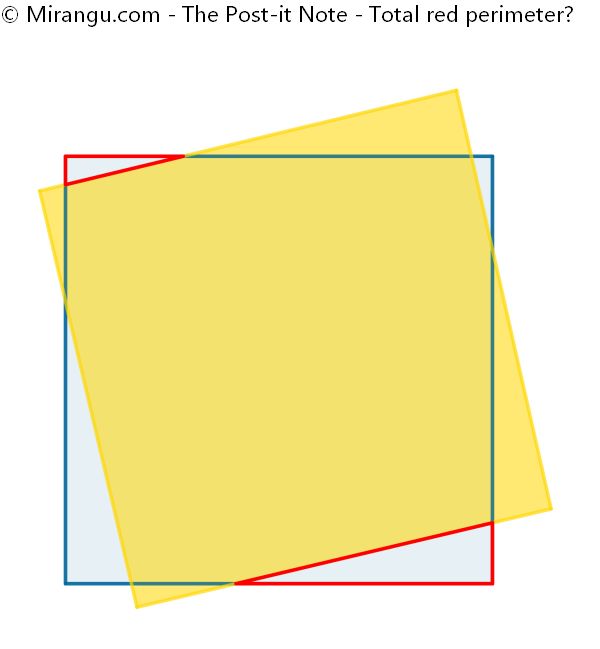
Two unit squares (having side 1) are placed as shown. What is the total perimeter of the two red triangles?

Solution

The total red perimeter is 2.

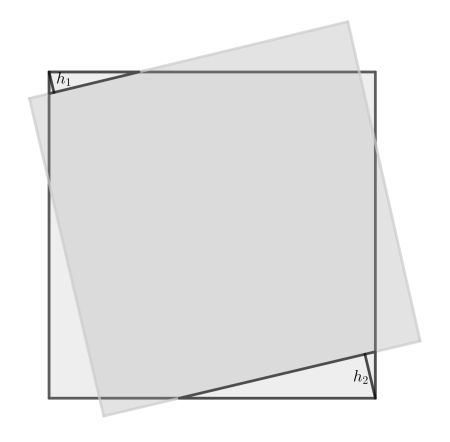
The proof consists of two parts. First we show that the yellow square can be translated without effect on the red perimeter. Then we compute the answer in case the centres of the squares coincide.

First acknowledge that the two right triangles are similar. Therefore their perimeter is a constant C times their height. So P_tot=C*(h₁+h₂). Now it is easy to see that under translations the sum of the heights does not vary. Therefore we are allowed to translate the square such that their centres coincide, without changing P_tot.

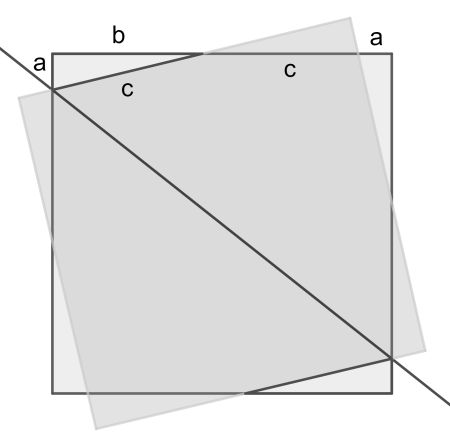
Now in this configuration we have a fourfold rotational symmetry and reflection symmetry in the line shown. Therefore, all eight triangles in the figure are congruent. Mark their sides as a, b and c. A single triangle has perimeter a+b+c, which from the diagram is seen to be also the length of a side, which is 1. Therefore P_tot=2.